在平面内给出了 $100$ 个点，其中没有三点在一条直线上．考察以上述点为顶点的所有可能的三角形，求证：这些三角形中至多只有 $70\%$ 的三角形是锐角三角形．（苏联）
【难度】
【出处】
1970年第12届IMO试题
【标注】
【答案】
略
【解析】
首先证明：在平面上任给无三点共线的 $5$ 个点，一定可以找到三个以它们为顶点的非锐角三角形．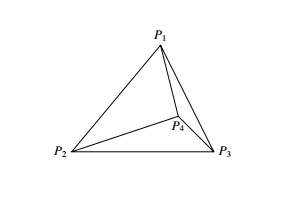
若 $5$ 个点 $P_1,P_2,P_3,P_4,P_5$ 的凸包三角形，不妨设为 $\triangle P_1P_2P_3$，则点 $P_4,P_5$ 在 $\triangle P_1P_2P_3$ 内．由于 $\angle P_1P_4P_2,\angle P_2P_4P_3,\angle P_3P_4P_1$ 中至少有两个非锐角，从而 $\triangle P_1P_4P_2 ,\triangle P_2P_4P_3 ,\triangle P_3P_4P_1 $ 中至少有两个非锐角三角形．同理，$\triangle P_1P_5P_2,\triangle P_2P_5P_3 ,\triangle P_3P_5P_1 $ 中也至少有两个非锐角三角形．所以，此时至少有 $4$ 个非锐角三角形．
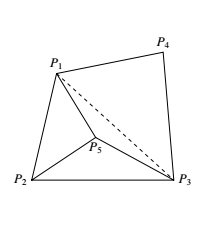若 $5$ 个点 $P_1,P_2,P_3,P_4,P_5$ 的凸包是四边形，不妨设为 $P_1P_2P_3P_4$，点 $P_5$ 在四边形 $P_1P_2P_3P_4$ 内部．由于 $\angle P_1P_2P_3,\angle P_2P_3P_4,\angle P_3P_4P_1,\angle P_4P_1P_2$ 中至少有一个非锐角，故 $\triangle P_1P_2P_3 ,\triangle P_2P_3P_4 ,\triangle P_3P_4P_1 $ 和 $\angle P_4P_1P_2$ 中至少有一个非锐角三角形．又不妨设点 $P_5$ 在 $\triangle P_1P_2P_4$ 内，则 $\triangle P_1P_2P_5,\triangle P_2P_3P_5 ,\triangle P_3P_1P_5 $ 中至少有两个非锐角三角形，从而此时至少有 $3$ 个非锐角三角形．
若 $5$ 个点的凸包是五边形 $P_1,P_2,P_3,P_4,P_5$，则 $\angle P_1P_2P_3,\angle P_2P_3P_4,\angle P_3P_4P_5,\angle P_4P_5P_1,\angle P_5P_1P_2$ 中至少有一个非锐角，故 $\triangle P_1P_2P_3 ,\triangle P_2P_3P_4 ,\triangle P_3P_4P_1 $ 和 $\angle P_4P_1P_2$ 中至少有两个非锐角，如果其余三个均为锐角，那么其中必定有两个是相邻的，不妨设 $\angle P_5P_1P_1$ 与 $\angle P_1P_2P_3$ 是两个相邻的锐角，于是 $\angle P_1P_5P_4 $ 与 $\angle P_2P_3P_5 $ 中至少有一个为非锐角，从而此时也至少有三个非锐角三角形．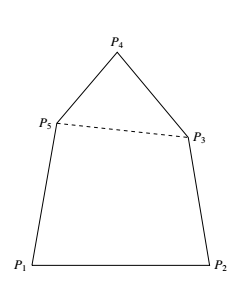
综上可知，平面上任给无三点共线的 $5$ 点，一定可以找到三个以它们为顶点的非锐角三角形．
由于每个非锐角三角形至多属于 $C_{100-3}^2$ 个 $5$ 点组，而 $5$ 点组共有 $C_{100}^5$，所以 $100$ 个点组成的非锐角三角形至少有 $\dfrac{3C_{100}^5}{C_{97}^2}$ 个，从而锐角三角形至多有 $C_{100}^3-\dfrac{3C_{100}^5}{C_{97}^2}$ 个，于是 $\dfrac{C_{100}^3-\frac{3C_{100}^5}{C_{97}^2}}{C_{100}^3}=1-\dfrac{3C_{100}^5}{C_{100}^3C_{97}^2}=\dfrac{7}{10}=70\%$，故命题可证．
若 $5$ 个点 $P_1,P_2,P_3,P_4,P_5$ 的凸包三角形，不妨设为 $\triangle P_1P_2P_3$，则点 $P_4,P_5$ 在 $\triangle P_1P_2P_3$ 内．由于 $\angle P_1P_4P_2,\angle P_2P_4P_3,\angle P_3P_4P_1$ 中至少有两个非锐角，从而 $\triangle P_1P_4P_2 ,\triangle P_2P_4P_3 ,\triangle P_3P_4P_1 $ 中至少有两个非锐角三角形．同理，$\triangle P_1P_5P_2,\triangle P_2P_5P_3 ,\triangle P_3P_5P_1 $ 中也至少有两个非锐角三角形．所以，此时至少有 $4$ 个非锐角三角形．若 $5$ 个点 $P_1,P_2,P_3,P_4,P_5$ 的凸包是四边形，不妨设为 $P_1P_2P_3P_4$，点 $P_5$ 在四边形 $P_1P_2P_3P_4$ 内部．由于 $\angle P_1P_2P_3,\angle P_2P_3P_4,\angle P_3P_4P_1,\angle P_4P_1P_2$ 中至少有一个非锐角，故 $\triangle P_1P_2P_3 ,\triangle P_2P_3P_4 ,\triangle P_3P_4P_1 $ 和 $\angle P_4P_1P_2$ 中至少有一个非锐角三角形．又不妨设点 $P_5$ 在 $\triangle P_1P_2P_4$ 内，则 $\triangle P_1P_2P_5,\triangle P_2P_3P_5 ,\triangle P_3P_1P_5 $ 中至少有两个非锐角三角形，从而此时至少有 $3$ 个非锐角三角形．若 $5$ 个点的凸包是五边形 $P_1,P_2,P_3,P_4,P_5$，则 $\angle P_1P_2P_3,\angle P_2P_3P_4,\angle P_3P_4P_5,\angle P_4P_5P_1,\angle P_5P_1P_2$ 中至少有一个非锐角，故 $\triangle P_1P_2P_3 ,\triangle P_2P_3P_4 ,\triangle P_3P_4P_1 $ 和 $\angle P_4P_1P_2$ 中至少有两个非锐角，如果其余三个均为锐角，那么其中必定有两个是相邻的，不妨设 $\angle P_5P_1P_1$ 与 $\angle P_1P_2P_3$ 是两个相邻的锐角，于是 $\angle P_1P_5P_4 $ 与 $\angle P_2P_3P_5 $ 中至少有一个为非锐角，从而此时也至少有三个非锐角三角形．
综上可知，平面上任给无三点共线的 $5$ 点，一定可以找到三个以它们为顶点的非锐角三角形．由于每个非锐角三角形至多属于 $C_{100-3}^2$ 个 $5$ 点组，而 $5$ 点组共有 $C_{100}^5$，所以 $100$ 个点组成的非锐角三角形至少有 $\dfrac{3C_{100}^5}{C_{97}^2}$ 个，从而锐角三角形至多有 $C_{100}^3-\dfrac{3C_{100}^5}{C_{97}^2}$ 个，于是 $\dfrac{C_{100}^3-\frac{3C_{100}^5}{C_{97}^2}}{C_{100}^3}=1-\dfrac{3C_{100}^5}{C_{100}^3C_{97}^2}=\dfrac{7}{10}=70\%$，故命题可证．
答案
解析
备注
