求证：只存在一个这样的三角形，它的三边之长为三个连续正整数，并且它的三个内角中有一个角为另一个内角的两倍．（罗马尼亚）
【难度】
【出处】
1968年第10届IMO试题
【标注】
【答案】
略
【解析】
如图，设 $\triangle ABC$ 中，$\angle C=2\angle B$．三边长为 $n-1,n,n+1$．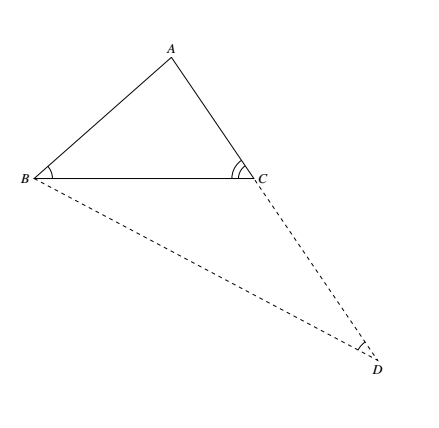
延长 $AC$ 至 $D$，联结 $BD$，且使 $BC=DC$．易知 $\angle D=\dfrac{1}{2} \angle C=\angle ABC$，于是 $\triangle ABC\sim\triangle ADB$．故 $AB^2=AC\cdot AD=AC\cdot (AC+BC)$．①
由于 $AB>AC$，故 $AB=n$ 或 $n+1$．
当 $AB=n$ 时，只能有 $AC=n-1,BC=n+1$，于是 ① 变成 $n^2=(n-1)\cdot 2n$ 或 $n=2$，此时三边不能组成三角形．
于是 $AB=n+1$，再分成两种情况．当 $AC=n,BC=n-1$ 时，有 $(n+1)^2=n(2n-1)$，此方程无正整数解；于是必有 $(n+1)^2=(n-1)(2n-1)$，得 $n=5$，即唯一解是边长为 $4,5,6$ 的三角形．
延长 $AC$ 至 $D$，联结 $BD$，且使 $BC=DC$．易知 $\angle D=\dfrac{1}{2} \angle C=\angle ABC$，于是 $\triangle ABC\sim\triangle ADB$．故 $AB^2=AC\cdot AD=AC\cdot (AC+BC)$．①由于 $AB>AC$，故 $AB=n$ 或 $n+1$．
当 $AB=n$ 时，只能有 $AC=n-1,BC=n+1$，于是 ① 变成 $n^2=(n-1)\cdot 2n$ 或 $n=2$，此时三边不能组成三角形．
于是 $AB=n+1$，再分成两种情况．当 $AC=n,BC=n-1$ 时，有 $(n+1)^2=n(2n-1)$，此方程无正整数解；于是必有 $(n+1)^2=(n-1)(2n-1)$，得 $n=5$，即唯一解是边长为 $4,5,6$ 的三角形．
答案
解析
备注
