在平行四边形 $ABCD$ 中，$\triangle ABD$ 为锐角三角形，$AB=a,AD=1,\angle BAD=\alpha$，$\odot A,\odot ,B\odot C,\odot D$ 分别为以平行四边形的顶点 $A、B、C、D$ 为圆心，以 $1$ 为半径的圆．求证：这 $4$ 个圆能够覆盖平行四边形 $ABCD$ 的充要条件是 $a\leqslant \cos \alpha+\sqrt{3}\sin \alpha$．（捷克斯洛伐克）
【难度】
【出处】
1967年第09届IMO试题
【标注】
【答案】
略
【解析】
设 $O$ 为 $\triangle ABD$ 的外心，它必在 $\triangle ABD$ 内部．又设外接圆半径为 $r$．若 $r>1$，则 $\odot A,\odot B,\odot D$ 不能覆盖 $O$，而 $\odot C$ 也不能覆盖 $O$．
这是因为（如图所示）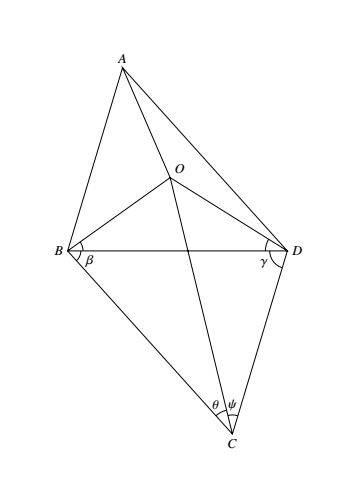
$\begin{aligned}
2\alpha+\beta+\gamma&=180^\circ-2(\theta+\psi)+\beta+\gamma\\
&>180\circ-2(\theta+\psi)+\theta+\psi\\
&=180^\circ-(\theta+\psi)\\
&>\theta +\psi
\end{aligned}$
这里用到了，$\beta,\gamma,\theta+\psi<90^circ$ 这些事实．
此即 $\angle OBC+\angle ODC>\angle BCD$，于是 $\angle OBC>\angle OCB,\angle ODC>\angle OCD$ 至少有一个成立．
因此 $OC>r$．
反之，若 $r\leqslant 1$，则 $O$ 被覆盖，又设 $P$ 为 $\triangle ABD$ 内任一点，它必在 $\triangle ABO,\triangle BDO,\triangle ADO$ 之一内，不妨设在 $\triangle ABO$ 内，则 $\min(AP,BP)\leqslant\dfrac{1}{2}(AP+BP)\leqslant \dfrac{1}{2}(AO+BO)=r\leqslant 1$，于是 $\triangle ABD$ 被覆盖，由对称性，$\triangle BCD$ 亦被覆盖．所以 $r\leqslant 1$ 是充要条件．
下面证明，$r\leqslant 1$ 等价于 $a\leqslant \cos\alpha+\sqrt{3}\sin\alpha$．
由余弦定理及正弦定理，知 $BD^2=1+a^2-2a\cos\alpha,BD=2r\sin\alpha$，
所以 $r\leqslant 1$ 当且仅当 $4\sin^2\alpha\geqslant 1+a^2-2a\cos\alpha$，
此即 $3\sin^2\alpha\geqslant (a\cos\alpha)^2$ ①
设 $DQ\perp AB$ 于 $Q$，由于 $\triangle ABD$ 是锐角三角形，故 $Q$ 在 $AB$ 内，于是 $\cos\alpha=AQ<AB=a$，① 等价于 $a-\cos\alpha\leqslant \sqrt{3}\sin\alpha$．
这是因为（如图所示）
$\begin{aligned}2\alpha+\beta+\gamma&=180^\circ-2(\theta+\psi)+\beta+\gamma\\
&>180\circ-2(\theta+\psi)+\theta+\psi\\
&=180^\circ-(\theta+\psi)\\
&>\theta +\psi
\end{aligned}$
这里用到了，$\beta,\gamma,\theta+\psi<90^circ$ 这些事实．
此即 $\angle OBC+\angle ODC>\angle BCD$，于是 $\angle OBC>\angle OCB,\angle ODC>\angle OCD$ 至少有一个成立．
因此 $OC>r$．
反之，若 $r\leqslant 1$，则 $O$ 被覆盖，又设 $P$ 为 $\triangle ABD$ 内任一点，它必在 $\triangle ABO,\triangle BDO,\triangle ADO$ 之一内，不妨设在 $\triangle ABO$ 内，则 $\min(AP,BP)\leqslant\dfrac{1}{2}(AP+BP)\leqslant \dfrac{1}{2}(AO+BO)=r\leqslant 1$，于是 $\triangle ABD$ 被覆盖，由对称性，$\triangle BCD$ 亦被覆盖．所以 $r\leqslant 1$ 是充要条件．
下面证明，$r\leqslant 1$ 等价于 $a\leqslant \cos\alpha+\sqrt{3}\sin\alpha$．
由余弦定理及正弦定理，知 $BD^2=1+a^2-2a\cos\alpha,BD=2r\sin\alpha$，
所以 $r\leqslant 1$ 当且仅当 $4\sin^2\alpha\geqslant 1+a^2-2a\cos\alpha$，
此即 $3\sin^2\alpha\geqslant (a\cos\alpha)^2$ ①
设 $DQ\perp AB$ 于 $Q$，由于 $\triangle ABD$ 是锐角三角形，故 $Q$ 在 $AB$ 内，于是 $\cos\alpha=AQ<AB=a$，① 等价于 $a-\cos\alpha\leqslant \sqrt{3}\sin\alpha$．
答案
解析
备注
