一个四面体，如果有且仅有一条棱长大于 $1$，求证这个四面体的体积不大于 $\dfrac{1}{8}$．（波兰）
【难度】
【出处】
1967年第09届IMO试题
【标注】
【答案】
略
【解析】
不妨设四面体为 $ABCD$，$\triangle ABC$ 的三边分别为 $AB=c,BC=a,CA=b$，且都小于 $1$，六条棱中，仅有 $AD>1$．
设 $A$ 至 $BC$ 之距为 $h$，则如图，作 $BC$ 的中垂线 $MN$，交 $BC$ 之平行线 $AN$ 于 $N$，则 $MN=h$（$M$ 为 $BC$ 中点）．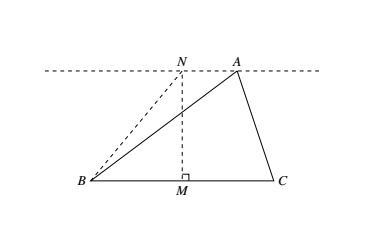
联结 $BN$，不妨设 $A$ 在 $BC$ 之右侧，则易知 $BN\leqslant BA\leqslant 1$，又由勾股定理，$h^2+\left(\dfrac{a}{2}\right)^2=BN^2$，于是 $h\leqslant\sqrt{1-\dfrac{a^2}{4}}$．
又设 $k$ 为 $\triangle BCD$ 的 $D$ 至 $BC$ 的高，同理可证 $k\leqslant \sqrt{1-\dfrac{a^2}{4}}$．
由于 $D$ 到底面 $\triangle ABC$ 的高 $\leqslant k$，于是
$\begin{aligned}
V_{ABCD}&\leqslant\dfrac{1}{3}S_{\triangle ABC}\cdot k\\
&=\dfrac{1}{6}ahk\leqslant\dfrac{1}{6}a\left(1-\dfrac{a^2}{4}\right)\\
&=\dfrac{1}{6}a\left(1-\dfrac{a}{2}\right)\left(1+\dfrac{a}{2}\right)
\end{aligned}$
因为 $a\leqslant 1$，故 $V_{ABCD}\leqslant\dfrac{1}{4}a\left(1-\dfrac{a}{2}\right)\leqslant \left(\dfrac{\frac{a}{2}+1-\frac{a}{2}}{2}\right)^2=\dfrac{1}{8}$
易知，若 $\triangle ABC$ 和 $\triangle DBC$ 是分别位于互相垂直的平面上且边长为 $1$ 的等边三角形，则 $V_{ABCD}=\dfrac{1}{8}$．
设 $A$ 至 $BC$ 之距为 $h$，则如图，作 $BC$ 的中垂线 $MN$，交 $BC$ 之平行线 $AN$ 于 $N$，则 $MN=h$（$M$ 为 $BC$ 中点）．
联结 $BN$，不妨设 $A$ 在 $BC$ 之右侧，则易知 $BN\leqslant BA\leqslant 1$，又由勾股定理，$h^2+\left(\dfrac{a}{2}\right)^2=BN^2$，于是 $h\leqslant\sqrt{1-\dfrac{a^2}{4}}$．又设 $k$ 为 $\triangle BCD$ 的 $D$ 至 $BC$ 的高，同理可证 $k\leqslant \sqrt{1-\dfrac{a^2}{4}}$．
由于 $D$ 到底面 $\triangle ABC$ 的高 $\leqslant k$，于是
$\begin{aligned}
V_{ABCD}&\leqslant\dfrac{1}{3}S_{\triangle ABC}\cdot k\\
&=\dfrac{1}{6}ahk\leqslant\dfrac{1}{6}a\left(1-\dfrac{a^2}{4}\right)\\
&=\dfrac{1}{6}a\left(1-\dfrac{a}{2}\right)\left(1+\dfrac{a}{2}\right)
\end{aligned}$
因为 $a\leqslant 1$，故 $V_{ABCD}\leqslant\dfrac{1}{4}a\left(1-\dfrac{a}{2}\right)\leqslant \left(\dfrac{\frac{a}{2}+1-\frac{a}{2}}{2}\right)^2=\dfrac{1}{8}$
易知，若 $\triangle ABC$ 和 $\triangle DBC$ 是分别位于互相垂直的平面上且边长为 $1$ 的等边三角形，则 $V_{ABCD}=\dfrac{1}{8}$．
答案
解析
备注
