已知两个锐角三角形 $\triangle {A}_{0}{B}_{0}{C}_{0}$ 与 $\triangle{A}_{1}{B}_{1}{C}_{1}$，求作一个三角形 $\triangle ABC$，使 $\triangle ABC\sim \triangle{A}_{1}{B}_{1}{C}_{1}$（$A,BC,$ 分别与 $A_1,B_1,C_1$ 相对应），$\triangle ABC$ 外接于 $\triangle {A}_{0}{B}_{0}{C}_{0}$（${A}_{0},{B}_{0},{C}_{0}$ 分别在 $BC,AC,AB$ 上），再求作满足上述条件的三角形中面积最大的一个．（意大利）
【难度】
【出处】
1967年第09届IMO试题
【标注】
【答案】
略
【解析】
分别以 $\triangle A_0B_0C_0$ 的边 $A_0C_0,A_0B_0$ 为弦，$\angle B_1$ 与 $\angle C_1$ 为圆周角做圆弧，如图所示．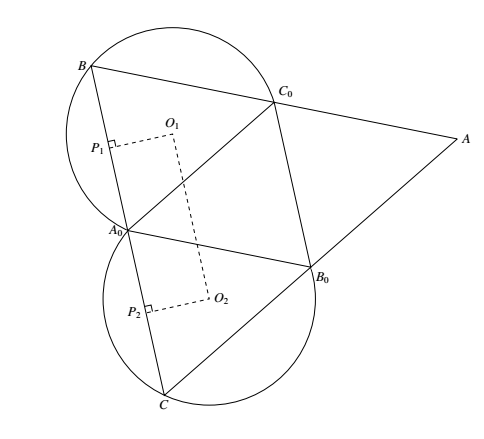
在两圆弧上分别取点 $B,C$，使 $B,A_0,C$ 在一直线上，延长 $BC_0,CB_0$ 交于 $A$，易知 $\angle A=\angle A_1$，于是 $\triangle ABC\sim\triangle A_1B_1C_1$．易知 $B$ 在 $\overparen{A_0C_0}$ 上任意，$C$ 依赖于 $B$．
又如图，设两圆弧圆心分别为 $O_1,O_2$，分别作 $O_1P_1,O_2P_2$ 与 $BC$ 垂直，$P_1,P_2$ 是垂足，于是 $P_1,P_2$ 分别为 $BA_0,A_0C$ 中点，于是 $BC=2P_1P_2\leqslant 2O_1O_2$．
等号成立，仅当 $BC\parallel O_1O_2$，由此不难定出满足条件的最大三角形的确切位置．
在两圆弧上分别取点 $B,C$，使 $B,A_0,C$ 在一直线上，延长 $BC_0,CB_0$ 交于 $A$，易知 $\angle A=\angle A_1$，于是 $\triangle ABC\sim\triangle A_1B_1C_1$．易知 $B$ 在 $\overparen{A_0C_0}$ 上任意，$C$ 依赖于 $B$．又如图，设两圆弧圆心分别为 $O_1,O_2$，分别作 $O_1P_1,O_2P_2$ 与 $BC$ 垂直，$P_1,P_2$ 是垂足，于是 $P_1,P_2$ 分别为 $BA_0,A_0C$ 中点，于是 $BC=2P_1P_2\leqslant 2O_1O_2$．
等号成立，仅当 $BC\parallel O_1O_2$，由此不难定出满足条件的最大三角形的确切位置．
答案
解析
备注
