在 $\triangle ABC$ 的三边 $AB,BC$ 与 $CA$ 上分别取点 $M,K,L $（不与 $\triangle ABC$ 的顶点重合）．求证：$\triangle MAL,\triangle KBM,\triangle LCK $ 中至少有一个的面积不大于 $\triangle ABC$ 面积的 $\dfrac{1}{4}$．（波兰）
【难度】
【出处】
1966年第08届IMO试题
【标注】
【答案】
略
【解析】
证法一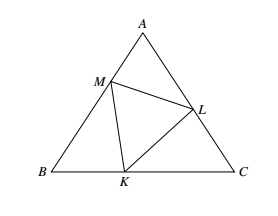
不妨设 $AB=c,BC=a,CA=b,LA=l,MB=m,KC=k$，易知
$\begin{aligned}
&S_{\triangle ALM}\cdot S_{\triangle MBK}\cdot S_{\triangle KCL}\\
&=\dfrac{1}{2}l(c-m)\sin A\cdot\dfrac{1}{2}m(a-k)\sin B\cdot\dfrac{1}{2}k(b-l)\sin C\\
&=\dfrac{1}{8}l(b-l)\cdot m(c-m)\cdot k(a-k)\sin A\sin B\sin C
\end{aligned}$
由基本不等式 $x(s-x)\leqslant\dfrac{(x+s-x)^2}{4}=\dfrac{s^2}{4}$ 知 $l(b-l)\leqslant\dfrac{b^2}{4},m(c-m)\leqslant\dfrac{c^2}{4},k(a-k)\leqslant\dfrac{a^2}{4}$，因此
$\begin{aligned}
&S_{\triangle ALM}\cdot S_{\triangle MBK}\cdot S_{\triangle KCL}\\
&=\dfrac{1}{512}a^2b^2c^2\sin A\sin B\sin C\\
&=\dfrac{1}{64}\cdot\dfrac{1}{2}ab\sin C\cdot\dfrac{1}{2}bc\sin A\cdot\dfrac{1}{2}ac\sin B\\
&=\left(\dfrac{1}{4}S_{\triangle ABC}\right)^3
\end{aligned}$
于是，$\min(S_{\triangle ALM},S_{\triangle MBK},S_{\triangle KCL})\leqslant\dfrac{1}{4}S_{\triangle ABC}$．
证法二
运用几何中的局部调整分析．运用一 极其简单的结论：如点 $A,B$ 在直线 $CD$ 同侧，且延长 $AB$ 同直线 $CD$ 相交，则 $S_{\triangle BCD}<S_{\triangle ACD}$．
下面开始证明，不妨设 $M$ 在 $AC^\prime $ 内，其中 $A^\prime,B^\prime,C^\prime$ 分别是 $BC,AC,AB$ 之中点．
若 $L$ 在 $AB^\prime$ 内 $S_{\triangle AML}\leqslant S_{\triangle AB^\prime C^\prime}=\dfrac{1}{4}S_{\triangle}$，问题已经解决，于是 $L$ 必在 $B^\prime C$ 内，同理 $K$ 必在 $A^\prime B$ 内，如图所示．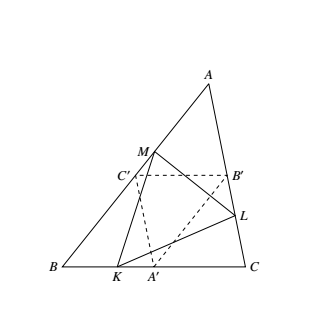
下面证明，在这种情况下，有 $S_{\triangle MKL}>\dfrac{1}{4}S_{\triangle ABC}$，于是由不等式性质知 $\min(S_{\triangle ALM},S_{\triangle MBK},S_{\triangle KCL})\leqslant\dfrac{1}{4}S_{\triangle ABC}$．
由于 $A^\prime C^\prime\parallel AC$，$KM$ 与 $A^\prime C^\prime$ 相交，易知延长 $KM$ 与 $AC$ 直线相交，于是 $S_{\triangle MKL}>S_{\triangle MKB^\prime}$，又 $A^\prime B^\prime\parallel AB$，易见延长 $B^\prime K$ 与 $AB$ 直线相交，于是 $S_{\triangle MKB^\prime}>S_{\triangle C^\prime KB^\prime}=\dfrac{1}{4}S_{\triangle ABC}$，根据上述两不等式，即知 $S_{\triangle MKL}>\dfrac{1}{4}S_{\triangle ABC}$．于是命题得证．
不妨设 $AB=c,BC=a,CA=b,LA=l,MB=m,KC=k$，易知$\begin{aligned}
&S_{\triangle ALM}\cdot S_{\triangle MBK}\cdot S_{\triangle KCL}\\
&=\dfrac{1}{2}l(c-m)\sin A\cdot\dfrac{1}{2}m(a-k)\sin B\cdot\dfrac{1}{2}k(b-l)\sin C\\
&=\dfrac{1}{8}l(b-l)\cdot m(c-m)\cdot k(a-k)\sin A\sin B\sin C
\end{aligned}$
由基本不等式 $x(s-x)\leqslant\dfrac{(x+s-x)^2}{4}=\dfrac{s^2}{4}$ 知 $l(b-l)\leqslant\dfrac{b^2}{4},m(c-m)\leqslant\dfrac{c^2}{4},k(a-k)\leqslant\dfrac{a^2}{4}$，因此
$\begin{aligned}
&S_{\triangle ALM}\cdot S_{\triangle MBK}\cdot S_{\triangle KCL}\\
&=\dfrac{1}{512}a^2b^2c^2\sin A\sin B\sin C\\
&=\dfrac{1}{64}\cdot\dfrac{1}{2}ab\sin C\cdot\dfrac{1}{2}bc\sin A\cdot\dfrac{1}{2}ac\sin B\\
&=\left(\dfrac{1}{4}S_{\triangle ABC}\right)^3
\end{aligned}$
于是，$\min(S_{\triangle ALM},S_{\triangle MBK},S_{\triangle KCL})\leqslant\dfrac{1}{4}S_{\triangle ABC}$．
证法二
运用几何中的局部调整分析．运用一 极其简单的结论：如点 $A,B$ 在直线 $CD$ 同侧，且延长 $AB$ 同直线 $CD$ 相交，则 $S_{\triangle BCD}<S_{\triangle ACD}$．
下面开始证明，不妨设 $M$ 在 $AC^\prime $ 内，其中 $A^\prime,B^\prime,C^\prime$ 分别是 $BC,AC,AB$ 之中点．
若 $L$ 在 $AB^\prime$ 内 $S_{\triangle AML}\leqslant S_{\triangle AB^\prime C^\prime}=\dfrac{1}{4}S_{\triangle}$，问题已经解决，于是 $L$ 必在 $B^\prime C$ 内，同理 $K$ 必在 $A^\prime B$ 内，如图所示．
下面证明，在这种情况下，有 $S_{\triangle MKL}>\dfrac{1}{4}S_{\triangle ABC}$，于是由不等式性质知 $\min(S_{\triangle ALM},S_{\triangle MBK},S_{\triangle KCL})\leqslant\dfrac{1}{4}S_{\triangle ABC}$．由于 $A^\prime C^\prime\parallel AC$，$KM$ 与 $A^\prime C^\prime$ 相交，易知延长 $KM$ 与 $AC$ 直线相交，于是 $S_{\triangle MKL}>S_{\triangle MKB^\prime}$，又 $A^\prime B^\prime\parallel AB$，易见延长 $B^\prime K$ 与 $AB$ 直线相交，于是 $S_{\triangle MKB^\prime}>S_{\triangle C^\prime KB^\prime}=\dfrac{1}{4}S_{\triangle ABC}$，根据上述两不等式，即知 $S_{\triangle MKL}>\dfrac{1}{4}S_{\triangle ABC}$．于是命题得证．
答案
解析
备注
