在 $\triangle OAB$ 中，已知 $\angle AOB$ 是锐角，从 $\triangle AOB$ 内或边上任一点 $M$（不与 $O$ 点重合），作 $MP\perp OA,MQ\perp OB$，垂足分别为 $P,Q$．$H$ 是 $\triangle OPQ$ 的垂心，分别求下列两种情况下 $H$ 的轨迹：
（$a$）当动点 $M$ 在线段 $AB$ 上运动时；
（$b$）当动点 $M$ 在 $\triangle OAB$ 的内部运动时．（罗马尼亚）
（$a$）当动点 $M$ 在线段 $AB$ 上运动时；
（$b$）当动点 $M$ 在 $\triangle OAB$ 的内部运动时．（罗马尼亚）
【难度】
【出处】
1965年第07届IMO试题
【标注】
【答案】
略
【解析】
（$a$）首先证明一个一般性的引理．
如图，在任意凸四边形 $AD-CB$ 中，$H,H^\prime$ 在 $CD$ 上，$M,P,Q$ 分别在 $AB,AD,BC$ 上，且 $QH^\prime \parallel BD\parallel MP,PH\parallel AC\parallel MQ$，则 $H$ 与 $H^\prime$ 重合，即平行四边形 $MPHQ$ 是内接的平行四边形．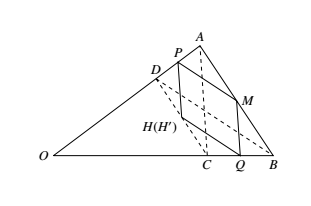
证明很简单，由于 $\dfrac{DH}{DC}=\dfrac{DP}{DA}=\dfrac{BM}{BA}=\dfrac{BQ}{BC}=\dfrac{DH^\prime}{DC}$，于是 $DH=DH^\prime $，因此 $H$ 与 $H^\prime $ 重合，引理证毕．
不妨设上述这些字母适用于本题（$a$），由 $AC\parallel MQ$ 知 $AC\perp OB$，同理 $BD\perp OA$．
因此 $H$ 即为 $\triangle OPQ$ 之垂心．
由于 $\dfrac{DH}{DC}=\dfrac{BM}{BA}$，当 $M$ 从 $B$ 跑至 $A$ 时，$H$ 从 $D$ 跑至 $C$．因此（$a$）的所求轨迹便是线段 $CD$．
注：当 $\triangle OAB$ 是直角或钝角三角形时，结论依然成立，不过 $CD$ 不一定在 $\triangle OAB$ 内部，同学们有兴趣可以画一个图看看．
（$b$）设 $M$ 为 $\triangle OAB$ 内一点．过 $M$ 作平行于 $AB$ 的直线分别交 $OA,OB$ 线段于内点 $A^\prime$ 和 $B^\prime$．易知，若作 $A^\prime C^\prime,B^\prime D^\prime$ 分别与 $OB,OA$ 垂直并分别交于 $C^\prime,D^\prime$，则线段 $A^\prime B^\prime$ 的内点与线段 $C^\prime D^\prime$ 的内点一一对应．
$\triangle OAB$ 的内点可看作在 $OA$ 和 $OB$ 的内点上一组平行于 $AB$ 的线段 $A^\prime B^\prime$ 的内点，因此对应点是 $OC$ 和 $OD$ 的内点上一组平行于 $CD$ 的 $C^\prime D^\prime$ 的内点．因此 $\triangle OAB$ 的内点集与 $\triangle OCD$ 的内点集一一对应，于是要求的 $H$ 点的轨迹是 $\triangle OCD$ 的内部．
如图，在任意凸四边形 $AD-CB$ 中，$H,H^\prime$ 在 $CD$ 上，$M,P,Q$ 分别在 $AB,AD,BC$ 上，且 $QH^\prime \parallel BD\parallel MP,PH\parallel AC\parallel MQ$，则 $H$ 与 $H^\prime$ 重合，即平行四边形 $MPHQ$ 是内接的平行四边形．
证明很简单，由于 $\dfrac{DH}{DC}=\dfrac{DP}{DA}=\dfrac{BM}{BA}=\dfrac{BQ}{BC}=\dfrac{DH^\prime}{DC}$，于是 $DH=DH^\prime $，因此 $H$ 与 $H^\prime $ 重合，引理证毕．不妨设上述这些字母适用于本题（$a$），由 $AC\parallel MQ$ 知 $AC\perp OB$，同理 $BD\perp OA$．
因此 $H$ 即为 $\triangle OPQ$ 之垂心．
由于 $\dfrac{DH}{DC}=\dfrac{BM}{BA}$，当 $M$ 从 $B$ 跑至 $A$ 时，$H$ 从 $D$ 跑至 $C$．因此（$a$）的所求轨迹便是线段 $CD$．
注：当 $\triangle OAB$ 是直角或钝角三角形时，结论依然成立，不过 $CD$ 不一定在 $\triangle OAB$ 内部，同学们有兴趣可以画一个图看看．
（$b$）设 $M$ 为 $\triangle OAB$ 内一点．过 $M$ 作平行于 $AB$ 的直线分别交 $OA,OB$ 线段于内点 $A^\prime$ 和 $B^\prime$．易知，若作 $A^\prime C^\prime,B^\prime D^\prime$ 分别与 $OB,OA$ 垂直并分别交于 $C^\prime,D^\prime$，则线段 $A^\prime B^\prime$ 的内点与线段 $C^\prime D^\prime$ 的内点一一对应．
$\triangle OAB$ 的内点可看作在 $OA$ 和 $OB$ 的内点上一组平行于 $AB$ 的线段 $A^\prime B^\prime$ 的内点，因此对应点是 $OC$ 和 $OD$ 的内点上一组平行于 $CD$ 的 $C^\prime D^\prime$ 的内点．因此 $\triangle OAB$ 的内点集与 $\triangle OCD$ 的内点集一一对应，于是要求的 $H$ 点的轨迹是 $\triangle OCD$ 的内部．
答案
解析
备注
