在平面上给出了 $n(\geqslant 3)$ 个点，$d$ 是其中每两点之间的距离的最大值，距离等于 $d$ 的两点所成的线段叫做这 $n$ 个点所组成的点集的直径．求证：这个点集的直径不多于 $n$ 条．（波兰）
【难度】
【出处】
1965年第07届IMO试题
【标注】
【答案】
略
【解析】
用反证法．假定直径多于 $n$ 条，如果从某个点出发的直径少于两条，我们把这点除去，剩下的 $n-1$ 个点至少有 $n$ 条直径，即此时点的数目仍比直径少，且 $n-1\geqslant 3$，故不妨假设从每一点出发的直径至少有两条．
由于直径数目比点多，而且每条直径都连结两个点，所以至少有一点（不妨设为 $A$）引出三条直径，设为 $AB,AC,AD$，每两条直径的夹角不超过 $60^\circ$，否则，$B,C,D$ 之间距离就会有大于 $d$．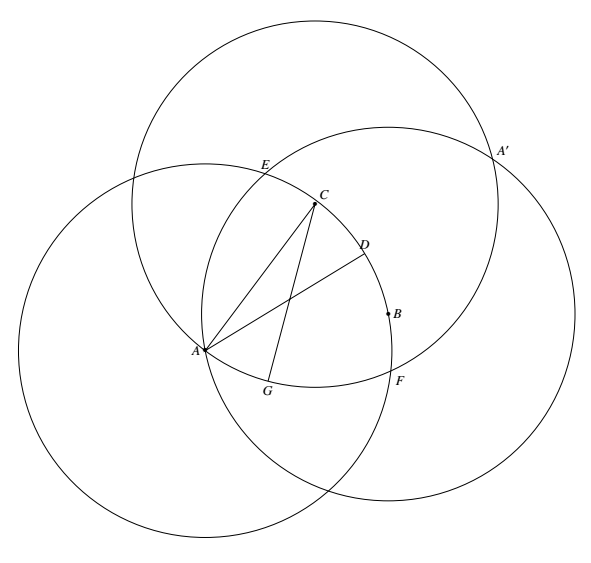
不妨设 $AD$ 在 $AB$ 与 $AC$ 之间，因此，$\odot (A,d)$（以 $A$ 为圆心，$d$ 为半径的圆），$\odot (B,d),\odot (C,d)$ 的公共部分覆盖了整个点集，而与 $D$ 的距离为 $d$ 的点只有点 $A$ 一个．事实上，在图中，对 $\overparen{AF}$ 上任一点 $G\ne A$，由于 $\angle GDC>\angle ADC=\angle ACD>\angle GCD$，所以 $DG<CG=d$．同理 $D$ 到除 $A$ 外的其他点距离都小于 $d$．
于是 $D$ 点只引出一条直径，矛盾．
由于直径数目比点多，而且每条直径都连结两个点，所以至少有一点（不妨设为 $A$）引出三条直径，设为 $AB,AC,AD$，每两条直径的夹角不超过 $60^\circ$，否则，$B,C,D$ 之间距离就会有大于 $d$．
不妨设 $AD$ 在 $AB$ 与 $AC$ 之间，因此，$\odot (A,d)$（以 $A$ 为圆心，$d$ 为半径的圆），$\odot (B,d),\odot (C,d)$ 的公共部分覆盖了整个点集，而与 $D$ 的距离为 $d$ 的点只有点 $A$ 一个．事实上，在图中，对 $\overparen{AF}$ 上任一点 $G\ne A$，由于 $\angle GDC>\angle ADC=\angle ACD>\angle GCD$，所以 $DG<CG=d$．同理 $D$ 到除 $A$ 外的其他点距离都小于 $d$．于是 $D$ 点只引出一条直径，矛盾．
答案
解析
备注
