在三边长分别为 $a、b、c$ 的 $\triangle ABC$ 内作内切圆，并作此圆的三条切线，它们分别平行于已知三角形的三边，这三条切线与已知三角形相截，得三个新的三角形，再分别作这三个三角形的内切圆，求所作出的四个圆的面积之和．（南斯拉夫）
【难度】
【出处】
1964年第06届IMO试题
【标注】
【答案】
略
【解析】
如图，设四个内切圆半径分别为 $r,r_a,r_b,r_c$，考虑 $\triangle APQ$，由于 $\triangle APQ\sim\triangle ABC$，故 $\dfrac{h_a-2r}{h_a}=\dfrac{r_a}{r}$，其中 $h_a$ 为 $\triangle BAC$ 的 $BC$ 边上的高．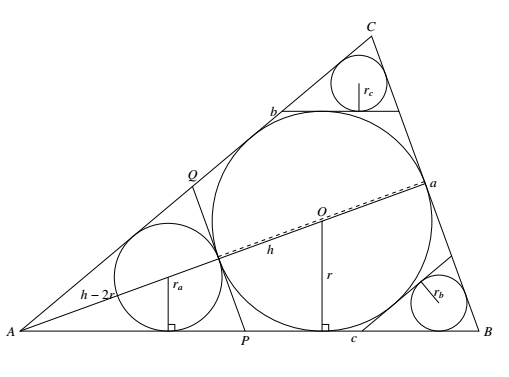
因此，所求面积为
$\displaystyle \begin{aligned}
&\pi r^2+\pi r^2\sum\left(\dfrac{h_a-2r}{h_a}\right)^2\\
&=\pi r^2\left(1+\sum\left(\dfrac{\frac{2S_{\triangle}}{a}-\frac{2S_{\triangle}}{p}}{\frac{2S_{\triangle}}{a}}\right)^2\right)\\
&=\pi r^2\left(1+\sum\left(\dfrac{p-a}{p}\right)^2\right)\\
&=\dfrac{\pi r^2}{p^2}(a^2+b^2+c^2)\\
&=\dfrac{\pi}{p^3}(p-a)(p-b)(p-c)(a^2+b^2+c^2)
\end{aligned}$
其中 $S_{\triangle}$ 为 $\triangle ABC$ 面积，$p=\dfrac{1}{2}(a+b+c)$．
因此，所求面积为$\displaystyle \begin{aligned}
&\pi r^2+\pi r^2\sum\left(\dfrac{h_a-2r}{h_a}\right)^2\\
&=\pi r^2\left(1+\sum\left(\dfrac{\frac{2S_{\triangle}}{a}-\frac{2S_{\triangle}}{p}}{\frac{2S_{\triangle}}{a}}\right)^2\right)\\
&=\pi r^2\left(1+\sum\left(\dfrac{p-a}{p}\right)^2\right)\\
&=\dfrac{\pi r^2}{p^2}(a^2+b^2+c^2)\\
&=\dfrac{\pi}{p^3}(p-a)(p-b)(p-c)(a^2+b^2+c^2)
\end{aligned}$
其中 $S_{\triangle}$ 为 $\triangle ABC$ 面积，$p=\dfrac{1}{2}(a+b+c)$．
答案
解析
备注
