求证：$\cos \dfrac{\pi }{7}-\cos \dfrac{2\pi }{7}+\cos \dfrac{3\pi }{7}=\dfrac{1}{2}$．（民主德国）
【难度】
【出处】
1963年第05届IMO试题
【标注】
【答案】
略
【解析】
证法一
利用余弦函数的积化和差公式，得
$\begin{aligned}
&2\cos\dfrac{\pi}{14}\left(\cos\dfrac{\pi}{7}-\cos\dfrac{2\pi}{7}+\cos\dfrac{3\pi}{7}\right)\\
&=\left(\cos\dfrac{3\pi}{14}+\cos\dfrac{\pi}{14}\right)
-\left(\cos\dfrac{5\pi}{14}+\cos\dfrac{3\pi}{14}\right)+\left(\cos\dfrac{7\pi}{14}+\cos\dfrac{5\pi}{14}\right)\\
&=\cos\dfrac{\pi}{14}(\ne 0)
\end{aligned}$
由此得证．
证法二
如图，作 $\angle MON=\dfrac{\pi}{7}$．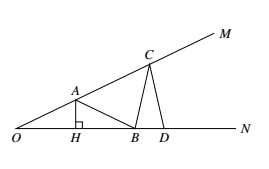
在 $OM$ 上取 $A$，使 $OA=1$，在 $ON$ 上取 $B(\ne O)$，使 $AB=1$，在 $OM$ 上再取 $C(\ne A)$，使 $BC=1$，再在 $ON$ 上取 $D$，使 $CD=1(D\ne B)$，则
$\angle CAB=\angle ACB=\dfrac{2\pi}{7}$
$\angle CBD=\angle CDB=\dfrac{3\pi}{7}$
于是 $\angle OCD=\dfrac{3\pi}{7},OC=OD$．
作 $AH\perp OB$，则 $OB=2OH=2\cos\dfrac{\pi}{7}$．
同理，$AC=2\cos\dfrac{2\pi}{7},BD=2\cos\dfrac{3\pi}{7}$．
由 $OA+AC=OC=OD=OB+BD$，得 $1+2\cos\dfrac{2\pi}{7}=2\cos\dfrac{\pi}{7}+2\cos\dfrac{3\pi}{7}$，
即 $\cos \dfrac{\pi }{7}-\cos \dfrac{2\pi }{7}+\cos \dfrac{3\pi }{7}=\dfrac{1}{2}$．
利用余弦函数的积化和差公式，得
$\begin{aligned}
&2\cos\dfrac{\pi}{14}\left(\cos\dfrac{\pi}{7}-\cos\dfrac{2\pi}{7}+\cos\dfrac{3\pi}{7}\right)\\
&=\left(\cos\dfrac{3\pi}{14}+\cos\dfrac{\pi}{14}\right)
-\left(\cos\dfrac{5\pi}{14}+\cos\dfrac{3\pi}{14}\right)+\left(\cos\dfrac{7\pi}{14}+\cos\dfrac{5\pi}{14}\right)\\
&=\cos\dfrac{\pi}{14}(\ne 0)
\end{aligned}$
由此得证．
证法二
如图，作 $\angle MON=\dfrac{\pi}{7}$．
在 $OM$ 上取 $A$，使 $OA=1$，在 $ON$ 上取 $B(\ne O)$，使 $AB=1$，在 $OM$ 上再取 $C(\ne A)$，使 $BC=1$，再在 $ON$ 上取 $D$，使 $CD=1(D\ne B)$，则$\angle CAB=\angle ACB=\dfrac{2\pi}{7}$
$\angle CBD=\angle CDB=\dfrac{3\pi}{7}$
于是 $\angle OCD=\dfrac{3\pi}{7},OC=OD$．
作 $AH\perp OB$，则 $OB=2OH=2\cos\dfrac{\pi}{7}$．
同理，$AC=2\cos\dfrac{2\pi}{7},BD=2\cos\dfrac{3\pi}{7}$．
由 $OA+AC=OC=OD=OB+BD$，得 $1+2\cos\dfrac{2\pi}{7}=2\cos\dfrac{\pi}{7}+2\cos\dfrac{3\pi}{7}$，
即 $\cos \dfrac{\pi }{7}-\cos \dfrac{2\pi }{7}+\cos \dfrac{3\pi }{7}=\dfrac{1}{2}$．
答案
解析
备注
