在空间中已知一直角的一边通过一已知点 $A$，而另一边与已知线段 $BC$ 至少有一公共点，求该直角顶点的轨迹．（苏联）
【难度】
【出处】
1963年第05届IMO试题
【标注】
【答案】
略
【解析】
按 $A$ 及线段 $BC$ 的位置关系分情况考察．
（1）若 $A$ 在线段 $BC$ 上，如图，分别以 $AB,AC$ 为直径作球．易知两球外没有满足要求的点存在；而球内任一点都有这样的点存在（图中的 $Q,Q^\prime$）．因此，这两个球及内部便是所求轨迹（包括线段 $BC$ 在内），当然，当 $A$ 与 $B,C$ 之一重合时，一球缩成一点．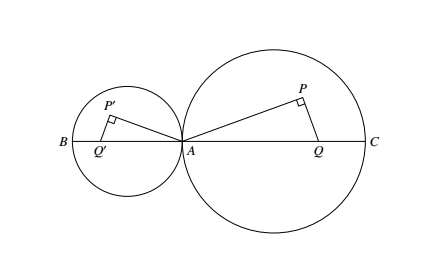
（2）若 $A$ 在 $BC$ 的延长线上，如图，不妨设 $B$ 介于 $A,C$ 之间．分别以 $AB,AC$ 为直径作二球，则所求轨迹是大球球面以及大球球内但不在小球内的点．这是因为，如果 $Q$ 是小球内的点，过 $Q$ 作垂直于 $AQ$ 的平面，与 $AC$ 的交点在 $AB$ 上而不在 $BC$ 上，而属于大球又非小球内的任一点 $P$，垂直于 $AP$ 的平面与 $BC$ 相交．
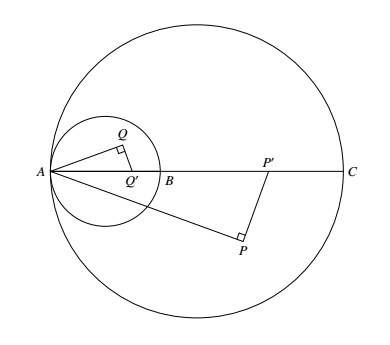（3）$A$ 点不在直线 $BC$ 上时，如图以 $AB$ 为直径作球 $\Omega_1$，以 $AC$ 为直径作球 $\Omega_1$，以 $AC$ 为直径作球 $\Omega_2$，易知凡在球面 $\Omega_1$ 或 $\Omega_2$ 上的点都属于所求的轨迹，凡在两球之外的任一点 $P$，与 $AP$ 垂直且过 $P$ 的平面既不与 $AB$ 相交，亦不与 $AC$ 相交．如此平面与 $ABC$ 平面平行，则不与 $BC$ 相交；否则设交线为 $l$，易知既然 $l$ 与 $AB,AC$ 均无公共点，自然与 $BC$ 也无公共点了．所以凡在两球之外的任意点，都不满足要求．
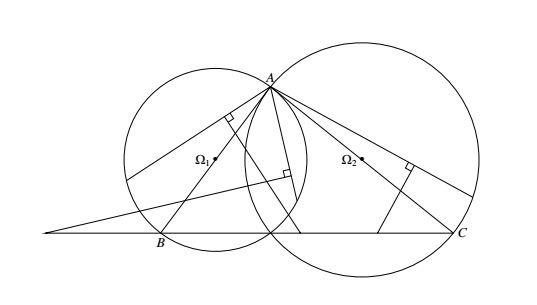又同时在球 $\Omega_1$ 与 $\Omega_2$ 内的点也不满足要求．这是因为，任找其中一点 $P$，垂直于 $AP$ 且过 $P$ 的平面必与 $AB,AC$ 均相交，交点不是 $B,C$，设此平面与 $ABC$ 平面交于 $l$，则 $l$ "穿"过 $AB,AC$ 内部，显然无法同 $BC$ 线段相交了，于是这类点不满足条件．
而在 $\Omega_1$ 内又不属 $\Omega_2$ 及其内的任一点 $P$ 则满足要求．此时垂直于 $AP$ 且过 $P$ 的平面必与 $AB$ 相交，不与 $AC$ 相交，于是此平面与平面 $ABC$ 的交线 $l$ "穿"过 $AB$，碰不到 $AC$，于是只好穿过 $BC$ 了．
同理，位于 $\Omega_2$ 内又不属 $\Omega_1$ 及其内部的任一点也满足要求．
综上所述，若令 $B_1,B_2$ 分别表示球 $\Omega_1,\Omega_2$ 内的点集，$B^\prime_1,B^\prime_2$ 分别表示球 $\Omega_1,\Omega_2$ 内及面上的点集，则所求轨迹为 $B_1^\prime\bigcup B_2^\prime\setminus B_1\bigcap B_2$．
（1）若 $A$ 在线段 $BC$ 上，如图，分别以 $AB,AC$ 为直径作球．易知两球外没有满足要求的点存在；而球内任一点都有这样的点存在（图中的 $Q,Q^\prime$）．因此，这两个球及内部便是所求轨迹（包括线段 $BC$ 在内），当然，当 $A$ 与 $B,C$ 之一重合时，一球缩成一点．
（2）若 $A$ 在 $BC$ 的延长线上，如图，不妨设 $B$ 介于 $A,C$ 之间．分别以 $AB,AC$ 为直径作二球，则所求轨迹是大球球面以及大球球内但不在小球内的点．这是因为，如果 $Q$ 是小球内的点，过 $Q$ 作垂直于 $AQ$ 的平面，与 $AC$ 的交点在 $AB$ 上而不在 $BC$ 上，而属于大球又非小球内的任一点 $P$，垂直于 $AP$ 的平面与 $BC$ 相交．（3）$A$ 点不在直线 $BC$ 上时，如图以 $AB$ 为直径作球 $\Omega_1$，以 $AC$ 为直径作球 $\Omega_1$，以 $AC$ 为直径作球 $\Omega_2$，易知凡在球面 $\Omega_1$ 或 $\Omega_2$ 上的点都属于所求的轨迹，凡在两球之外的任一点 $P$，与 $AP$ 垂直且过 $P$ 的平面既不与 $AB$ 相交，亦不与 $AC$ 相交．如此平面与 $ABC$ 平面平行，则不与 $BC$ 相交；否则设交线为 $l$，易知既然 $l$ 与 $AB,AC$ 均无公共点，自然与 $BC$ 也无公共点了．所以凡在两球之外的任意点，都不满足要求．又同时在球 $\Omega_1$ 与 $\Omega_2$ 内的点也不满足要求．这是因为，任找其中一点 $P$，垂直于 $AP$ 且过 $P$ 的平面必与 $AB,AC$ 均相交，交点不是 $B,C$，设此平面与 $ABC$ 平面交于 $l$，则 $l$ "穿"过 $AB,AC$ 内部，显然无法同 $BC$ 线段相交了，于是这类点不满足条件．而在 $\Omega_1$ 内又不属 $\Omega_2$ 及其内的任一点 $P$ 则满足要求．此时垂直于 $AP$ 且过 $P$ 的平面必与 $AB$ 相交，不与 $AC$ 相交，于是此平面与平面 $ABC$ 的交线 $l$ "穿"过 $AB$，碰不到 $AC$，于是只好穿过 $BC$ 了．
同理，位于 $\Omega_2$ 内又不属 $\Omega_1$ 及其内部的任一点也满足要求．
综上所述，若令 $B_1,B_2$ 分别表示球 $\Omega_1,\Omega_2$ 内的点集，$B^\prime_1,B^\prime_2$ 分别表示球 $\Omega_1,\Omega_2$ 内及面上的点集，则所求轨迹为 $B_1^\prime\bigcup B_2^\prime\setminus B_1\bigcap B_2$．
答案
解析
备注
