设 $A、B、C$ 为圆周 $K$ 上的三个已知点，试用尺规作图求出圆周上第四点 $D$，使四边形 $ABCD$ 存在内切圆。（保加利亚）
【难度】
【出处】
1962年第04届IMO试题
【标注】
【答案】
略
【解析】
证法一
如图，假定 $D$ 已作出，则内切圆圆心 $I$ 位于 $\angle A,\angle B,\angle C$ 的平分线上．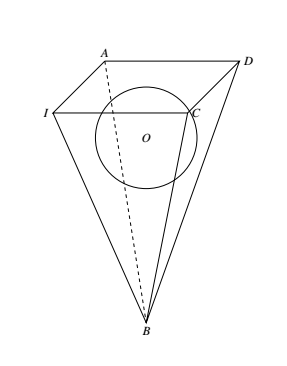
易见
$\begin{aligned}
\angle AIC&=\angle IAB+\angle ABC+\angle ICB\\
&\dfrac{1}{2}(\angle A+\angle C)+\angle ABC\\
&=90^\circ+\angle ABC
\end{aligned}$
（当 $\angle ABC>90^circ时,\angle AIC$ 为优角）．
于是，可以 $ AC $ 为弦，$ \angle ABC+90^\circ$ 为张角作弧，又作 $\angle ABC$ 的角平分线交此弧于 $I$．联结 $AI,CI$，作 $\angle DAI=\angle BAI,\angle DCI=\angle BCI$，于是 $D$ 即为所求．
证明如下：
因为 $\angle AIC=90^\circ+\angle ABC=\dfrac{1}{2}(\angle DAB+\angle DCB)+\angle ABC$
所以 $\angle DAB+\angle DCB=180^\circ$
故 $A,B,C,D$ 四点共圆，圆周上的 $D$ 点即为所求．
讨论：设 $P$ 是弧 $\overparen{AC}$ 上任一点，当 $P=A$ 时，$AB+PC>AP+BC$；当 $P=C$ 时，$AB+PC<AP+BC$，由连续性知，必有 $\overparen{AC}$ 上一点 $P^\prime$，满足 $AB+CP^\prime=AP^\prime+BC$．
故本题必有解．
证法二
凸四边形 $ABCD$ 有内切圆的充要条件是 $AB+CD=AD+BC$．
如图，不妨设 $BC\geqslant AB$，于是 $CD-AD=BC-AB=$ 定长，$D$ 在一双曲线上．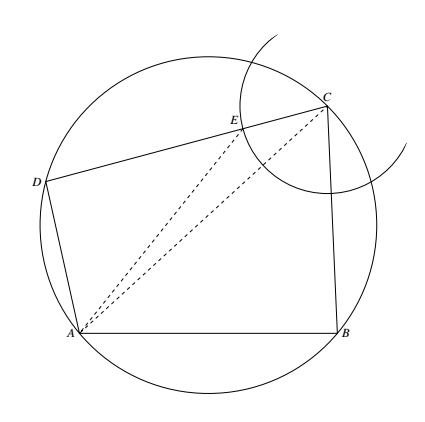
作法：（1）如 $BC=AB$，于是 $CD=AD$，$D$ 为 $AC$ 中垂线与 $\overparen{AC}$ 的交点．
（2）如 $BC>AB$．在 $CD$ 上取一点 $E$，使 $DE=AD$，于是
$\begin{aligned}
EC&=CD-DE\\
&=DC-AD\\
&=BC-AB
\end{aligned}$
$\begin{aligned}
\angle AEC&=180^\circ-\angle AED\\
&=180^\circ-\left(90^\circ-\dfrac{1}{2}\angle ADC\right)\\
&=90^\circ+\dfrac{1}{2}\angle ADC\\
&=90^\circ+\dfrac{1}{2}(180^\circ-\angle B)\\
&=180^\circ-\dfrac{1}{2}\angle B
\end{aligned}$
于是 $D$ 依赖于 $E$，只要以 $C$ 为圆心，$CE=BC-AB$ 为半径作圆 $\odot C$，又作圆弧 $\overparen{AEC}$，以 $AC$ 为弦，$180^\circ-\dfrac{1}{2}-\angle B$ 为张角，此弧与 $\odot C$ 的交点即为 $E$，由此再作出 $D$，证明略．
如图，假定 $D$ 已作出，则内切圆圆心 $I$ 位于 $\angle A,\angle B,\angle C$ 的平分线上．
易见$\begin{aligned}
\angle AIC&=\angle IAB+\angle ABC+\angle ICB\\
&\dfrac{1}{2}(\angle A+\angle C)+\angle ABC\\
&=90^\circ+\angle ABC
\end{aligned}$
（当 $\angle ABC>90^circ时,\angle AIC$ 为优角）．
于是，可以 $ AC $ 为弦，$ \angle ABC+90^\circ$ 为张角作弧，又作 $\angle ABC$ 的角平分线交此弧于 $I$．联结 $AI,CI$，作 $\angle DAI=\angle BAI,\angle DCI=\angle BCI$，于是 $D$ 即为所求．
证明如下：
因为 $\angle AIC=90^\circ+\angle ABC=\dfrac{1}{2}(\angle DAB+\angle DCB)+\angle ABC$
所以 $\angle DAB+\angle DCB=180^\circ$
故 $A,B,C,D$ 四点共圆，圆周上的 $D$ 点即为所求．
讨论：设 $P$ 是弧 $\overparen{AC}$ 上任一点，当 $P=A$ 时，$AB+PC>AP+BC$；当 $P=C$ 时，$AB+PC<AP+BC$，由连续性知，必有 $\overparen{AC}$ 上一点 $P^\prime$，满足 $AB+CP^\prime=AP^\prime+BC$．
故本题必有解．
证法二
凸四边形 $ABCD$ 有内切圆的充要条件是 $AB+CD=AD+BC$．
如图，不妨设 $BC\geqslant AB$，于是 $CD-AD=BC-AB=$ 定长，$D$ 在一双曲线上．
作法：（1）如 $BC=AB$，于是 $CD=AD$，$D$ 为 $AC$ 中垂线与 $\overparen{AC}$ 的交点．（2）如 $BC>AB$．在 $CD$ 上取一点 $E$，使 $DE=AD$，于是
$\begin{aligned}
EC&=CD-DE\\
&=DC-AD\\
&=BC-AB
\end{aligned}$
$\begin{aligned}
\angle AEC&=180^\circ-\angle AED\\
&=180^\circ-\left(90^\circ-\dfrac{1}{2}\angle ADC\right)\\
&=90^\circ+\dfrac{1}{2}\angle ADC\\
&=90^\circ+\dfrac{1}{2}(180^\circ-\angle B)\\
&=180^\circ-\dfrac{1}{2}\angle B
\end{aligned}$
于是 $D$ 依赖于 $E$，只要以 $C$ 为圆心，$CE=BC-AB$ 为半径作圆 $\odot C$，又作圆弧 $\overparen{AEC}$，以 $AC$ 为弦，$180^\circ-\dfrac{1}{2}-\angle B$ 为张角，此弧与 $\odot C$ 的交点即为 $E$，由此再作出 $D$，证明略．
答案
解析
备注
