已知 $\triangle ABC$ 为等腰三角形，$R$ 是其外接圆半径，$r$ 是它的内切圆半径．求证：这两圆心之间的距离为 $d=\sqrt{R(R-2r)}$．（民主德国）
【难度】
【出处】
1962年第04届IMO试题
【标注】
【答案】
略
【解析】
本题结论对任意三角形（不限于等腰三角形）均成立（即欧拉公式）．
如图，设 $O,S$ 分别为 $\triangle ABC$ 的外心和内心．联结 $AS$ 并延长交 $\odot O$ 于 $D$．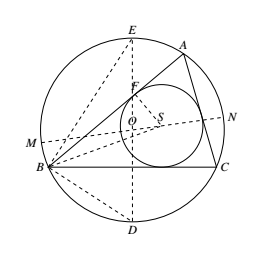
作直径 $DE$，联结 $BD,BE,FS$（$F$ 为内切圆与 $AB$ 之切点），$BS,OS$ 并延长交 $\odot O$ 于 $M,N$．
设 $OS=d$，则
$\begin{aligned}
d^2&=R^2-(R^2-d^2)\\
&=R^2-(R+d)(R-d)\\
&=R^2-MS\cdot NS\\
&=R^2-AS\cdot SD
\end{aligned}$
接下来显然只需证 $AS\cdot SD=2Rr$ 即可．
易见 $\triangle BED\sim\triangle FAS$，故 $BD\cdot AS=ED\cdot FS=2Rr$．
于是，问题又简化到只需证明 $BD=SD$．
由于
$\begin{aligned}
\angle SBD&=\angle SBC+\angle CBD\\
&=\dfrac{1}{2}\angle ABC+\angle DAC\\
&=\dfrac{1}{2}(\angle ABC+\angle BAC)
\end{aligned}$
又 $\angle BSD=\angle ABS+\angle BAS=\dfrac{1}{2}(\angle ABC+\angle BAC)$，
命题得证，结论成立．
如图，设 $O,S$ 分别为 $\triangle ABC$ 的外心和内心．联结 $AS$ 并延长交 $\odot O$ 于 $D$．
作直径 $DE$，联结 $BD,BE,FS$（$F$ 为内切圆与 $AB$ 之切点），$BS,OS$ 并延长交 $\odot O$ 于 $M,N$．设 $OS=d$，则
$\begin{aligned}
d^2&=R^2-(R^2-d^2)\\
&=R^2-(R+d)(R-d)\\
&=R^2-MS\cdot NS\\
&=R^2-AS\cdot SD
\end{aligned}$
接下来显然只需证 $AS\cdot SD=2Rr$ 即可．
易见 $\triangle BED\sim\triangle FAS$，故 $BD\cdot AS=ED\cdot FS=2Rr$．
于是，问题又简化到只需证明 $BD=SD$．
由于
$\begin{aligned}
\angle SBD&=\angle SBC+\angle CBD\\
&=\dfrac{1}{2}\angle ABC+\angle DAC\\
&=\dfrac{1}{2}(\angle ABC+\angle BAC)
\end{aligned}$
又 $\angle BSD=\angle ABS+\angle BAS=\dfrac{1}{2}(\angle ABC+\angle BAC)$，
命题得证，结论成立．
答案
解析
备注
