已知 $\triangle {P}_{1}{P}_{2}{P}_{3}$ 及三角形内任一点 $P$,直线 ${P}_{1}P,{P}_{2}P,{P}_{3}P$ 分别与交对边于 ${Q}_{1},{Q}_{2},{Q}_{3}$.求证:在 $\dfrac{{{P}_{1}}P}{P{{Q}_{1}}},\dfrac{{{P}_{2}}P}{P{{Q}_{2}}},\dfrac{{{P}_{3}}P}{P{{Q}_{3}}}$ 这三个比值中,至少有一个不大于 $2$,也至少有一个不小于 $2$.(民主德国)
【难度】
【出处】
1961年第03届IMO试题
【标注】
【答案】
略
【解析】
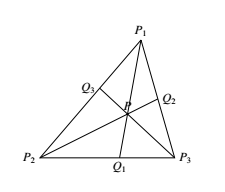 易知
易知$\begin{aligned}
\dfrac{PQ_1}{P_1Q_1}&=\dfrac{S_{\triangle PP_2P_3}}{S_{\triangle P_1P_2P_3}}\\
\dfrac{PQ_2}{P_2Q_2}&=\dfrac{S_{\triangle PP_1P_3}}{S_{\triangle P_1P_2P_3}}\\
\dfrac{PQ_3}{P_3Q_3}&=\dfrac{S_{\triangle PP_1P_2}}{S_{\triangle P_1P_2P_3}}\\
\end{aligned}$
于是 $\dfrac{PQ_1}{P_1Q_1}+\dfrac{PQ_2}{P_2Q_2}+\dfrac{PQ_3}{P_3Q_3}=1$
于是,必有一者 $\geqslant \dfrac{1}{3}$,也必有一者 $\leqslant\dfrac{1}{3}$,不妨设 $\dfrac{PQ_1}{P_1Q_1}\geqslant\dfrac{1}{3},\dfrac{PQ_2}{P_2Q_2}\leqslant\dfrac{1}{3}$,
此即 $\dfrac{P_1P}{PQ_1}\leqslant 2,\dfrac{P_2P}{PQ_2}\geqslant 2$.
答案
解析
备注