求作 $\triangle ABC$ 使 $AC=b,AB=c,\angle AMB=\alpha<90^\circ$，这里 $M$ 是 $BC$ 的中点，并由此证明：当且仅当 $b\tan \dfrac{\alpha}{2}\leqslant c<b$ 时，本题有解．又在什么情况下等号成立？（捷克斯洛伐克）
【难度】
【出处】
1961年第03届IMO试题
【标注】
【答案】
略
【解析】
如图，设 $D$ 是 $AC$ 中点，则 $MD=\dfrac{AB}{2}=\dfrac{c}{2},\angle AMC=180^\circ-\alpha$，于是，可以 $AC$ 为弦，$180^\circ-\alpha$ 为圆周角作弧 $\overparen{AC}$，再以 $D$ 为圆心，$DM$ 为半径作圆，与 $\overparen{AC}$ 交于 $M$（一般可能会有两个），联结 $CM$ 并延长一倍至 $B$，$\triangle ABC$ 即为所求．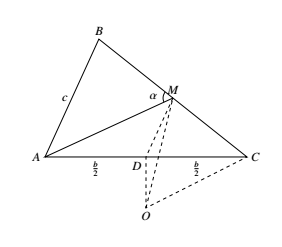
由作法知，欲使 $\triangle ABC$ 存在，仅当 $M$ 这个圆弧与圆弧的交点存在，今找出 $\triangle AMC$ 之外心 $O$，$O$ 在 $\triangle AMC$ 外，易知 $\angle DOC=\alpha<90^\circ$．
$M$ 存在的条件也就是 $0\leqslant \angle DOM<\alpha$，或 $\cos\alpha<\cos\angle DOM\leqslant 1$，这由余弦定理，就是 $\cos\alpha<\dfrac{DO^2+MO^2-DM^2}{2DO\cdot MO}\leqslant 1$．
易知 $MO=CO=\dfrac{b}{2\sin\alpha},DO=\dfrac{b}{2}\cot\alpha,DM=\dfrac{c}{2}$，代入不等式，得
$\cos\alpha<\dfrac{\frac{b^2}{\sin^2\alpha}+b^2\cot^2\alpha-c^2}{2b^2\frac{\cos\alpha}{\sin^2\alpha}}\leqslant 1$
化简，得 $\cos\alpha<\dfrac{1+\cos^2\alpha-\frac{c^2}{b^2}\sin^2\alpha}{2\cos\alpha}\leqslant 1$
左式即 $\dfrac{c^2}{b^2}\sin^2\alpha<1-\cos^2\alpha=\sin^2\alpha$ 即 $c<b$；
右式即 $1+\cos^2\alpha-2\cos\alpha\leqslant\dfrac{c^2}{b^2}\sin^2\alpha$ 或 $1-\cos\alpha\leqslant\dfrac{c}{b}\sin\alpha$
此即 $b\tan\dfrac{\alpha}{2}=b\dfrac{1-\cos\alpha}{\sin\alpha}\leqslant c$．
所以本题得证．
由作法知，欲使 $\triangle ABC$ 存在，仅当 $M$ 这个圆弧与圆弧的交点存在，今找出 $\triangle AMC$ 之外心 $O$，$O$ 在 $\triangle AMC$ 外，易知 $\angle DOC=\alpha<90^\circ$．$M$ 存在的条件也就是 $0\leqslant \angle DOM<\alpha$，或 $\cos\alpha<\cos\angle DOM\leqslant 1$，这由余弦定理，就是 $\cos\alpha<\dfrac{DO^2+MO^2-DM^2}{2DO\cdot MO}\leqslant 1$．
易知 $MO=CO=\dfrac{b}{2\sin\alpha},DO=\dfrac{b}{2}\cot\alpha,DM=\dfrac{c}{2}$，代入不等式，得
$\cos\alpha<\dfrac{\frac{b^2}{\sin^2\alpha}+b^2\cot^2\alpha-c^2}{2b^2\frac{\cos\alpha}{\sin^2\alpha}}\leqslant 1$
化简，得 $\cos\alpha<\dfrac{1+\cos^2\alpha-\frac{c^2}{b^2}\sin^2\alpha}{2\cos\alpha}\leqslant 1$
左式即 $\dfrac{c^2}{b^2}\sin^2\alpha<1-\cos^2\alpha=\sin^2\alpha$ 即 $c<b$；
右式即 $1+\cos^2\alpha-2\cos\alpha\leqslant\dfrac{c^2}{b^2}\sin^2\alpha$ 或 $1-\cos\alpha\leqslant\dfrac{c}{b}\sin\alpha$
此即 $b\tan\dfrac{\alpha}{2}=b\dfrac{1-\cos\alpha}{\sin\alpha}\leqslant c$．
所以本题得证．
答案
解析
备注
