已知直角三角形 $ABC$，将斜边 $BC$ $n$ 等分，$n$ 是奇数．设含有斜边中点的那段对于 $A$ 所成的张角为 $\alpha$，$\triangle ABC$ 斜边 $BC=a$，斜边上的高为 $h$．求证：$\tan \alpha =\dfrac{4nh}{\left( {{n}^{2}}-1 \right)a}$．（罗马尼亚）
【难度】
【出处】
1960年第02届IMO试题
【标注】
【答案】
略
【解析】
不妨设中间那一段为 $PQ$，易知 $BC$ 之中点 $O$ 也是 $PQ$ 的中点，如图所示．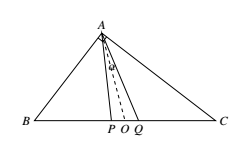
由中线长公式，知 $AP^2+AQ^2=\dfrac{1}{2}PQ^2+2AO^2=\left(\dfrac{1}{2n^2}+\dfrac{1}{2}\right)a^2$．
又由余弦定理，知
$\begin{aligned}
&AP\cdot AQ\cdot \cos\alpha\\
&=\dfrac{1}{2}(AP^2+AQ^2-PQ^2)\\
&=\dfrac{1}{4}\left(1-\dfrac{1}{n^2}\right)a^2
\end{aligned}$
而由面积知
$\begin{aligned}
\dfrac{1}{2}AP\cdot AQ\cdot \sin\alpha&=S_{\triangle APQ}\\
&=\dfrac{1}{n}S_{\triangle ABC}\\
&=\dfrac{1}{2n}ah
\end{aligned}$
② $\div$ ① 得 $\tan\alpha=\dfrac{4ah}{n\left(1-\dfrac{1}{n^2}\right)a^2}=\dfrac{4nh}{(n^2-1)a}$．
由中线长公式，知 $AP^2+AQ^2=\dfrac{1}{2}PQ^2+2AO^2=\left(\dfrac{1}{2n^2}+\dfrac{1}{2}\right)a^2$．又由余弦定理，知
$\begin{aligned}
&AP\cdot AQ\cdot \cos\alpha\\
&=\dfrac{1}{2}(AP^2+AQ^2-PQ^2)\\
&=\dfrac{1}{4}\left(1-\dfrac{1}{n^2}\right)a^2
\end{aligned}$
而由面积知
$\begin{aligned}
\dfrac{1}{2}AP\cdot AQ\cdot \sin\alpha&=S_{\triangle APQ}\\
&=\dfrac{1}{n}S_{\triangle ABC}\\
&=\dfrac{1}{2n}ah
\end{aligned}$
② $\div$ ① 得 $\tan\alpha=\dfrac{4ah}{n\left(1-\dfrac{1}{n^2}\right)a^2}=\dfrac{4nh}{(n^2-1)a}$．
答案
解析
备注
