已知三条线段长分别为 $h_a、h_b$ 和 $m_a$，求作 $\triangle ABC$，使 $BC,AC$ 边上的高分别为 $h_a,h_b,BC$ 边上的中线为 ${m}_{a}$．（匈牙利）
【难度】
【出处】
1960年第02届IMO试题
【标注】
【答案】
略
【解析】
先作直角三角形 $\triangle AHM$，使：$AH\perp HM,AH=h_a,AM=m_a$．
以 $M$ 为圆心，$\dfrac{1}{2}h_b$ 为半径作 $\odot M$．
如图所示，再过 $A$ 作 $\odot M$ 的切线，切点分别为 $D,D^\prime$．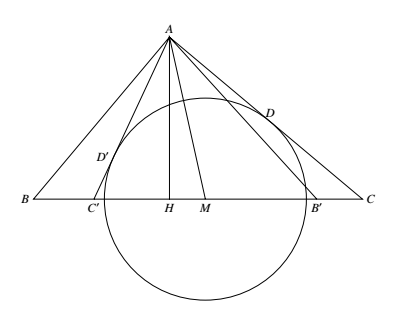
如果延长 $AD$ 与 $HM$ 直线相交，就设此交点为 $C$，并作 $C$ 关于 $M$ 的对称点 $B$，易知 $B$ 至 $AC$ 的距离就是 $2MD=h_b$，于是 $\triangle ABC$ 即为所求．如图所示同样得到 $\triangle AB^\prime C^\prime$．
但是并非所有的 $h_a,h_b$ 和 $m_a$ 都导致两解．首先，有解必须 $m_a\geqslant h_a$，在此前提下，易知：若 $h_a>\dfrac{1}{2}h_b$，则 $m_a>h_a$ 有两解而 $m_a=h_a$ 有一解；若 $h_a\leqslant\dfrac{1}{2}h_b<m_a$，有一解；若 $h_a\leqslant \dfrac{1}{2}h_b=m_a$，则 $m_a>h_a$ 有一解而 $m_a=h_a$ 无解；$\dfrac{1}{2}h_b>m_a$ 时无解．
以 $M$ 为圆心，$\dfrac{1}{2}h_b$ 为半径作 $\odot M$．
如图所示，再过 $A$ 作 $\odot M$ 的切线，切点分别为 $D,D^\prime$．
如果延长 $AD$ 与 $HM$ 直线相交，就设此交点为 $C$，并作 $C$ 关于 $M$ 的对称点 $B$，易知 $B$ 至 $AC$ 的距离就是 $2MD=h_b$，于是 $\triangle ABC$ 即为所求．如图所示同样得到 $\triangle AB^\prime C^\prime$．但是并非所有的 $h_a,h_b$ 和 $m_a$ 都导致两解．首先，有解必须 $m_a\geqslant h_a$，在此前提下，易知：若 $h_a>\dfrac{1}{2}h_b$，则 $m_a>h_a$ 有两解而 $m_a=h_a$ 有一解；若 $h_a\leqslant\dfrac{1}{2}h_b<m_a$，有一解；若 $h_a\leqslant \dfrac{1}{2}h_b=m_a$，则 $m_a>h_a$ 有一解而 $m_a=h_a$ 无解；$\dfrac{1}{2}h_b>m_a$ 时无解．
答案
解析
备注
