已知一等腰梯形，它的两底和高分别为 $a,b$ 和 $h$．
（$a$）在梯形的对称轴上求作一点 $P$，使这点对梯形的腰所张的视角为直角．
（$b$）求 $P$ 点到梯形两底边的距离．
（$c$）在什么条件下，点 $P$ 能够作出（即讨论点 $P$ 在什么情况下存在）．（保加利亚）
（$a$）在梯形的对称轴上求作一点 $P$，使这点对梯形的腰所张的视角为直角．
（$b$）求 $P$ 点到梯形两底边的距离．
（$c$）在什么条件下，点 $P$ 能够作出（即讨论点 $P$ 在什么情况下存在）．（保加利亚）
【难度】
【出处】
1960年第02届IMO试题
【标注】
【答案】
略
【解析】
如图，设等腰梯形上底 $AD$，下底 $BC$ 分别为 $a$ 和 $b$，高为 $h$，$MN$ 为梯形 $ABCD$ 的对称轴．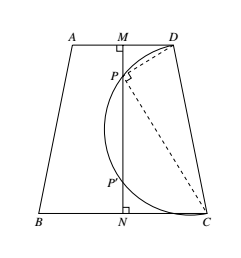
如 $\angle DPC=90^\circ$，$P$ 必在以 $CD$ 为直径的圆上．
（$a$）今以 $CD$ 为直径作圆，交对称轴 $MN$ 于两点（$P$ 和 $P^\prime$），或交于一点 $P$，或没有交点．
（$b$）易知 $Rt\triangle DMP\sim Rt\triangle PNC$，因此有 $\begin{cases}
PM\cdot PN=MD\cdot NC=\dfrac{ab}{4}\\
PM+PN=h
\end{cases}$
根据韦达定理，$PM,PN$ 为方程 $x^2-hx+\dfrac{ab}{4}=0$ 的两根．
并且由韦达定理看出，只要上述二次方程有根，必定是两正根．于是，仅当 $\Delta\geqslant 0$ 时，$P$ 存在，即 $h^2-ab\geqslant 0,x=\dfrac{h}{2}\pm\sqrt{h^2-ab}$．
其中一个根为 $PM$，另一个等于 $PN$．
（$c$）由（$b$）知，
如果 $h^2<ab$，交点 $P$ 不存在，即以 $CD$ 为直径的圆不与线段 $MN$ 相交；
如果 $h^2=ab$，只有一个点 $P$ 位于 $MN$ 的中点，此时圆与 $MN$ 相切；
如果 $h^2>ab$，有两个点 $P,P^\prime$ 满足条件，即圆与线段 $MN$ 相交．比如图示，可认为
$PM=P^\prime N=\dfrac{h}{2}-\sqrt{h^2-ab}$
$PN=P^\prime M=\dfrac{h}{2}+\sqrt{h^2-ab}$
如 $\angle DPC=90^\circ$，$P$ 必在以 $CD$ 为直径的圆上．（$a$）今以 $CD$ 为直径作圆，交对称轴 $MN$ 于两点（$P$ 和 $P^\prime$），或交于一点 $P$，或没有交点．
（$b$）易知 $Rt\triangle DMP\sim Rt\triangle PNC$，因此有 $\begin{cases}
PM\cdot PN=MD\cdot NC=\dfrac{ab}{4}\\
PM+PN=h
\end{cases}$
根据韦达定理，$PM,PN$ 为方程 $x^2-hx+\dfrac{ab}{4}=0$ 的两根．
并且由韦达定理看出，只要上述二次方程有根，必定是两正根．于是，仅当 $\Delta\geqslant 0$ 时，$P$ 存在，即 $h^2-ab\geqslant 0,x=\dfrac{h}{2}\pm\sqrt{h^2-ab}$．
其中一个根为 $PM$，另一个等于 $PN$．
（$c$）由（$b$）知，
如果 $h^2<ab$，交点 $P$ 不存在，即以 $CD$ 为直径的圆不与线段 $MN$ 相交；
如果 $h^2=ab$，只有一个点 $P$ 位于 $MN$ 的中点，此时圆与 $MN$ 相切；
如果 $h^2>ab$，有两个点 $P,P^\prime$ 满足条件，即圆与线段 $MN$ 相交．比如图示，可认为
$PM=P^\prime N=\dfrac{h}{2}-\sqrt{h^2-ab}$
$PN=P^\prime M=\dfrac{h}{2}+\sqrt{h^2-ab}$
答案
解析
备注
