两个平面 $P$ 和 $Q$ 相交于直线 $p$，已知点 $A$ 在平面 $P$ 内而不在平面 $Q$ 内，$C$ 在平面 $Q$ 内而不在平面 $P$ 内，且都不在 $p$ 上．求作一四边形 $ABCD$ 满足 $AB\parallel CD,AD=BC$，且点 $B$ 在平面 $P$ 内，点 $D$ 在平面 $Q$ 内，并使这个四边形存在内切圆．（捷克斯洛伐克）
【难度】
【出处】
1959年第01届IMO试题
【标注】
【答案】
略
【解析】
首先证明 $AB,CD$ 均与 $p$ 平行．这是因为如设 $p$ 上一点为 $M$，过 $M$ 仅有一条直线 $l$ 与 $AB,CD$ 平行，由于 $l$ 既在 $P$ 内又在 $Q$ 内，于是 $l=p$．
如图，分别过 $A,C$ 作 $p$ 的平行线 $AB,CD$．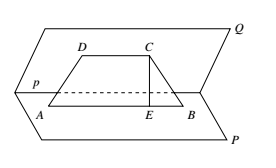
在 $AB,CD$ 所成平面内，作 $CE\perp AB$，垂足为 $E$，易知
$AE=\dfrac{1}{2}(AB+CD)=\dfrac{1}{2}(AD+BC)=AD$．
因此，可以 $A$ 为圆心，$AE$ 为半径作圆交 $CD$ 于 $D$，再进一步确定 $B$ 即可．
当 $AE>CE$ 时，本题有两解；当 $AE=CE$ 时，本题一解（这时梯形 $ABCD$ 变成了正方形）；当 $AE<CE$ 时，无解．
如图，分别过 $A,C$ 作 $p$ 的平行线 $AB,CD$．
在 $AB,CD$ 所成平面内，作 $CE\perp AB$，垂足为 $E$，易知$AE=\dfrac{1}{2}(AB+CD)=\dfrac{1}{2}(AD+BC)=AD$．
因此，可以 $A$ 为圆心，$AE$ 为半径作圆交 $CD$ 于 $D$，再进一步确定 $B$ 即可．
当 $AE>CE$ 时，本题有两解；当 $AE=CE$ 时，本题一解（这时梯形 $ABCD$ 变成了正方形）；当 $AE<CE$ 时，无解．
答案
解析
备注
