一个有 $2019$ 名用户的社交网络，这些用户中有某些人是好友关系，这里的好友关系是 相互的．下述事件在他们之中反复发生，且一段时间内只发生一次：
有三个用户 $A,B,C$ 满足 $ A$ 是 $B$ 与 $C$ 的共同好友且 $B,C$ 间没有好友关系，在事件发生时，$B,C$ 成为好友且 $A$ 与 $B$，$C$ 均解除好友关系．其它的好友关系均保持不变．
开始时，有 $1010$ 个用户每人有 $1009$ 个好友，另外的 $1009$ 个用户每人有 $1010$ 个好友．证明：存在一个事件序列使得其发生之后每个用户至多有一个好友．（克罗地亚）
有三个用户 $A,B,C$ 满足 $ A$ 是 $B$ 与 $C$ 的共同好友且 $B,C$ 间没有好友关系，在事件发生时，$B,C$ 成为好友且 $A$ 与 $B$，$C$ 均解除好友关系．其它的好友关系均保持不变．
开始时，有 $1010$ 个用户每人有 $1009$ 个好友，另外的 $1009$ 个用户每人有 $1010$ 个好友．证明：存在一个事件序列使得其发生之后每个用户至多有一个好友．（克罗地亚）
【难度】
【出处】
2019年第60届IMO试题
【标注】
【答案】
略
【解析】
证法一
我们先固定一些定义和记号：
1．若一个图所有点的度数都是偶数，那么我们称这个图为一个偶图．$m$ 个点的偶图记为 $E_m$．
2．$n$ 个点的完全图记为 $K_n$．
3．如果一个图 $G$ 的所有连通分支中没有 $K_n$（$n\geqslant 3$）或者 $E_m$（$m\geqslant 4$），那么我们称图 $G$ 是好的，不是好图的图称为坏的．
4．若一个操作 $T:G\Rightarrow G'$ 使得 $G'$ 的连通分支数比 $G$ 的连通分支数多 $1$，那么我们称 $T$ 为一个撕裂操作．
引理1：题设中的图 $G$ 是一个好图．
引理1的证明：首先 $G$ 中没有 $K_{1011}$，因为度数为 $1010$ 的点只有 $1009$ 个，完全不够．其次若 $G$ 中有一个 $K_{1010}$ 的连通分支，那么任何一个度数为 $1010$ 的点都不能与度数为 $1009$ 的点连在一次，但是这不可能，因为度数为 $1010$ 的点无法互相连线使得他们的度数都是 $1010$．
其次，若 $G$ 中有一个连通分支为一个偶图 $E_m$，那么这些 $E_m$ 中的点的度数只能是 $1010$．但是每一个度数为 $1010$ 的点必然要与一个度数为 $1009$ 的点相邻，那么 $E_m$ 中有度数为奇数的点，矛盾．引理1得证．
于是我们接下来证明：若一个好图 $G$ 可以继续操作，那么我们一定可以找到一种操作 $T:G\Rightarrow G'$ 使得 $G'$ 也是一个好图．若一个好图不可继续操作，那么显然这个图只能有单点或 $K_2$，即所有人至多认识一个人．而由于每次操作会使总边数 $-1$，所以这种操作最终总会停止，所以一定有一种方法使得所有人至多认识一个人，题目得证．
引理2：若一个操作 $T:G\Rightarrow G'$ 使得 $G$ 是好图而 $G'$ 是坏图，那么这个操作一定是撕裂操作．
引理2的证明：记录 $G'$ 的连通分支为 $G'_1 , \ldots , G'_k$，不妨 $G'_1$ 为一个 $K_n$ 或 $E_m$．若 $T$ 不是撕裂操作，那么 $G'_1 , \ldots , G'_k$ 的原像 $G_1 , \ldots , G_k$ 即是 $G$ 的所有连通分支．则 $G'_1$ 不可能是 $K_n$，这是因为操作 $T:G_1 \Rightarrow G'_1$ 只能使得 $G_1$ 的边数减小，而 $G'_1$ 不可能再加上任何边．
若 $G'_1$ 是一个偶图，由于操作 $T:G_1 \Rightarrow G'_1$ 不会改变点的奇偶性，那么 $G_1$ 本身也是个偶图，这与 $G$ 本身是个好图相矛盾．引理2证毕．
回到原题．我们用反证法，假设 $G$ 是一个好图，而所有 $G$ 上的操作 $T$ 都只能将 $G$ 变为一个坏图 $G'$．然后我们分情况推出矛盾．
情况1．若 $T$ 产生了一个 $K_n$．
情况1．1．如图：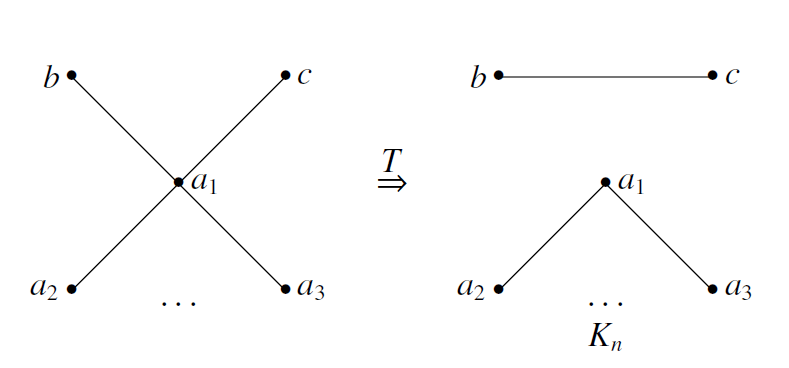
在这种情况，由于 $T$ 是撕裂的，它将 $K_n$ 独立出来，则 $a_2 , \ldots , a_n$ 都与 $b,c$ 无边，否则与引理2矛盾，则这是我们考虑 $T'$：
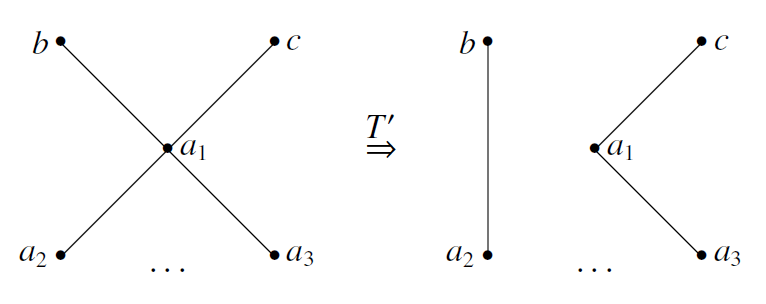此时 $a_1 , a_2$ 无边，$b,c$ 无边，$T'$ 并不会形成一个完全图的连通分支，若新生成的这个分支是一个偶图，则显然原像也是一个偶图，矛盾．
故 $T'(G)$ 是一个好图，矛盾．
情况1．2．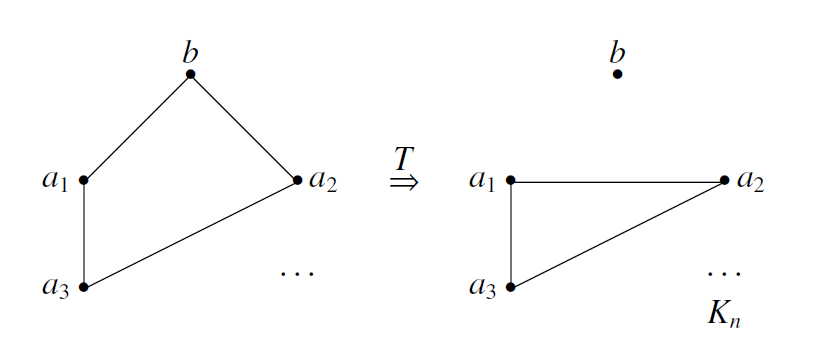
若 $n\geqslant 4$，则考虑 $T'$：
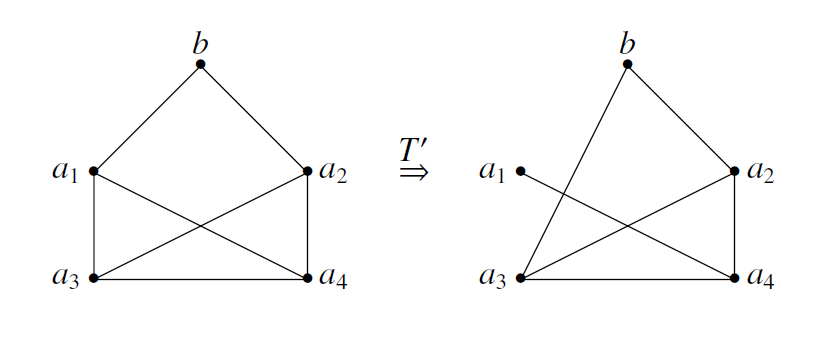由 $b$ 与 $a_4$ 无边，则新生成图无完全的连通分支，矛盾．
若 $n=3$，则只能是：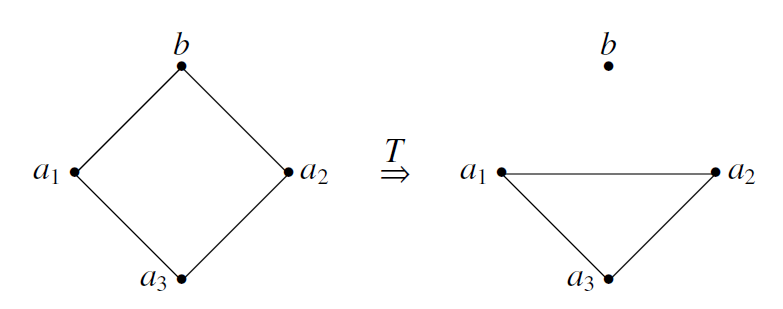
若 $b$ 与其他点都不相邻，则 $G$ 本身含有 $(b,a_1 , a_2 , a_3 )$ 这个偶图，矛盾．
所以 $b$ 必然与其他点相邻，不妨是 $c$，则我们考虑操作 $T'$：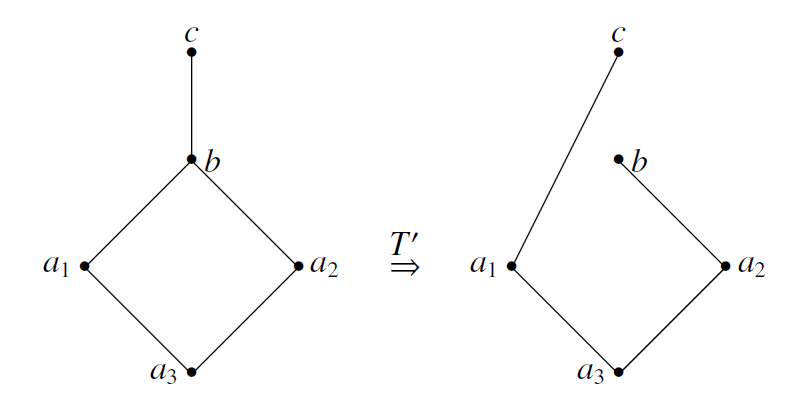
若这个图是个偶图，则原像也是个偶图，则 $G$ 是坏的，矛盾．
所以 $T'(G)$ 是好的，矛盾．
情况2．$T$ 会生成一个 $E_m$（$m\geqslant 4$），
情况2．1．如图：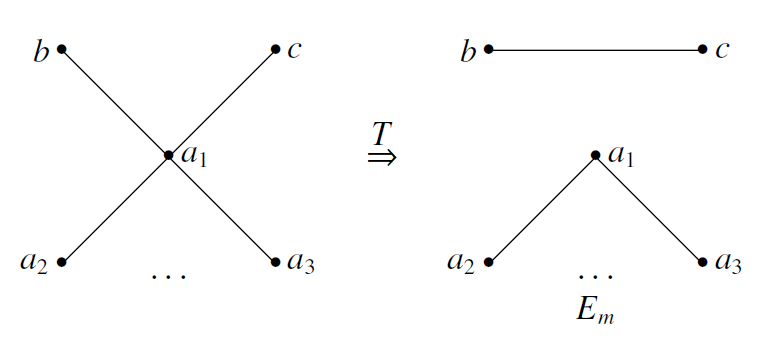
则我们考虑另外的操作 $T'$：
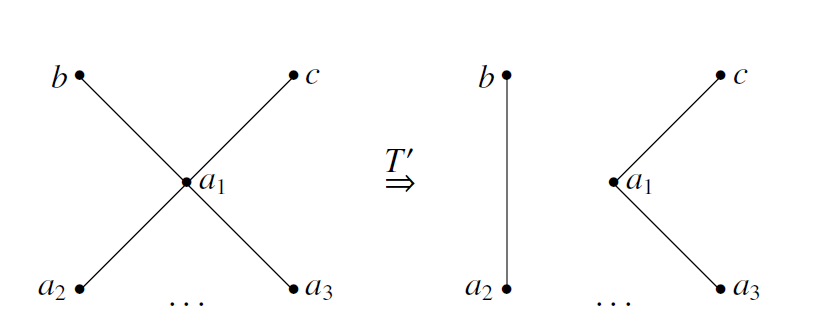同样的理由知，这个新的图不是偶图，且显然不会是一个完全图，所以 $T'(G)$ 是一个好图，矛盾．
情况2．2．如图：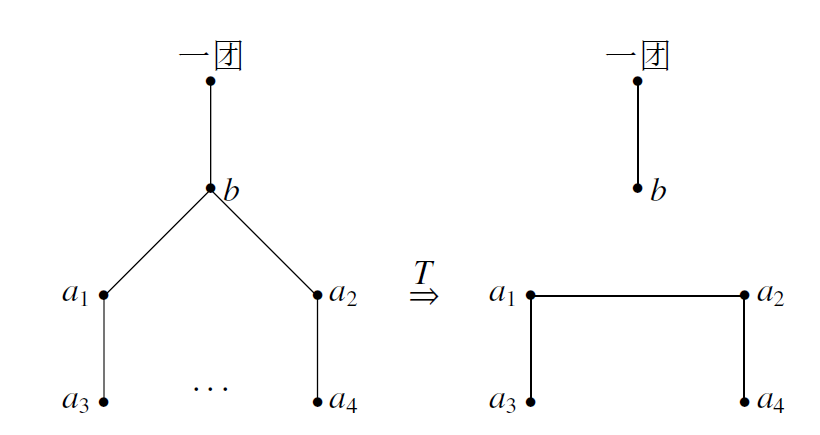
这时我们考虑另外一种操作 $T'$：
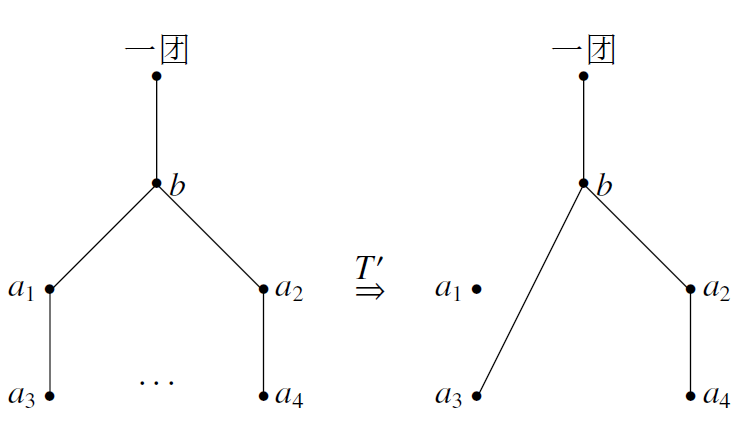所以若 $($ 一团 $,b,a_2 , \ldots , a_n )$ 是一个偶图，则原来的 $($ 一团 $,b,a_1,\ldots,a_n )$ 也是一个偶图，矛盾．
所以 $T'(G)$ 是一个好图，矛盾．
综上，命题成立．
证法二
用图论的语音来描述这个问题，有一个 $2019$ 阶简单图，其中 $1010$ 个顶点的度为 $1009$，$1009$ 个顶点的度为 $1010$．允许进行如下操作，如果有三个顶点 $A,B,C$ 满足 $AB,AC$ 是边，而 $BC$ 不是边，则可删去边 $AB,AC$，添上边 $BC$．要证明，存在一个操作序列，使得操作结束后，这个图变为若干条不相邻的边，以及一些孤立顶点．
由于 $G$ 中任意两个顶点 $u,v$ 的度之和不小于 $2018$，要么 $u,v$ 相邻，要么 $u,v$ 有公共的邻点，因此 $G$ 是连通的，且 $G$ 显然不是完全图，并且有顶点的度为奇数．事实上．结论对一个连通的非完全图，且有顶点的度为奇数的图都成立．下面仅假设 $G$ 是这样的一个图．
第一步：若 $G$ 不是树，则可通过若干次操作，使得图变为树．注意到操作不改变顶点的度的奇偶性，因此有度为奇数的顶点这一性质始终保持．只需说明若不是树，可通过一次操作使得图仍是连通的，这样由于每次操作减少一条边，必定在有限次操作后该图变为树．
取 $G$ 中的最大圈 $x_1,x_2,\cdots,x_k,x_1$．若这个圈不是哈密顿（Hamilton）圈，则存在一个顶点，不妨设是 $x_1$，它与不在该圈上的某个顶点 $y$ 相邻，于是 $y$ 不与 $x_2$ 相邻，否则就有个更大的圈 $x_1,y,x_2,\cdots,x_k,x_1$．删去边 $x_1y,x_1x_2$ 添上边 $yx_2$ 后，得到的图仍是连通的．
若这个圈是哈密顿圈，由于有奇数度的顶点，因此整个图不能只是这个圈，也不是完全图，因此存在一条弦，不妨设 $x_1x_i$，满足 $x_1,x_{i+1}$ 不相邻，或者 $x_1,x_{i-1}$ 不相邻．不妨设 $x_1,x_{i+1}$ 不相邻，那么可以删去 $x_1x_i,x_ix_{i+1}$，添上边 $x_1x_{i+1}$，得到的图仍是连通的．
第二步：若 $G$ 是树，则可通过若干次操作，使得图变为若干条不相邻的边，以及一些孤立顶点．如果 $G$ 只有一个或两个顶点，结论已经成立．假设 $G$ 至少含有三个顶点，则存在一个顶点 $u$，度至少是 $2$．设 $uv,uw$ 是 $u$ 处的两条边，则 $v,w$ 不相邻，删去边 $uv,uw$（此时变为三个连通分支），再添上边 $vw$，此时图有两个连通分支，并且每个连通分支仍是树．对至少含有三个顶点的连通分支再作同样的操作，直至每个连通分支都含有一个或两个顶点，这便是我们所需的结果．
我们先固定一些定义和记号：
1．若一个图所有点的度数都是偶数，那么我们称这个图为一个偶图．$m$ 个点的偶图记为 $E_m$．
2．$n$ 个点的完全图记为 $K_n$．
3．如果一个图 $G$ 的所有连通分支中没有 $K_n$（$n\geqslant 3$）或者 $E_m$（$m\geqslant 4$），那么我们称图 $G$ 是好的，不是好图的图称为坏的．
4．若一个操作 $T:G\Rightarrow G'$ 使得 $G'$ 的连通分支数比 $G$ 的连通分支数多 $1$，那么我们称 $T$ 为一个撕裂操作．
引理1：题设中的图 $G$ 是一个好图．
引理1的证明：首先 $G$ 中没有 $K_{1011}$，因为度数为 $1010$ 的点只有 $1009$ 个，完全不够．其次若 $G$ 中有一个 $K_{1010}$ 的连通分支，那么任何一个度数为 $1010$ 的点都不能与度数为 $1009$ 的点连在一次，但是这不可能，因为度数为 $1010$ 的点无法互相连线使得他们的度数都是 $1010$．
其次，若 $G$ 中有一个连通分支为一个偶图 $E_m$，那么这些 $E_m$ 中的点的度数只能是 $1010$．但是每一个度数为 $1010$ 的点必然要与一个度数为 $1009$ 的点相邻，那么 $E_m$ 中有度数为奇数的点，矛盾．引理1得证．
于是我们接下来证明：若一个好图 $G$ 可以继续操作，那么我们一定可以找到一种操作 $T:G\Rightarrow G'$ 使得 $G'$ 也是一个好图．若一个好图不可继续操作，那么显然这个图只能有单点或 $K_2$，即所有人至多认识一个人．而由于每次操作会使总边数 $-1$，所以这种操作最终总会停止，所以一定有一种方法使得所有人至多认识一个人，题目得证．
引理2：若一个操作 $T:G\Rightarrow G'$ 使得 $G$ 是好图而 $G'$ 是坏图，那么这个操作一定是撕裂操作．
引理2的证明：记录 $G'$ 的连通分支为 $G'_1 , \ldots , G'_k$，不妨 $G'_1$ 为一个 $K_n$ 或 $E_m$．若 $T$ 不是撕裂操作，那么 $G'_1 , \ldots , G'_k$ 的原像 $G_1 , \ldots , G_k$ 即是 $G$ 的所有连通分支．则 $G'_1$ 不可能是 $K_n$，这是因为操作 $T:G_1 \Rightarrow G'_1$ 只能使得 $G_1$ 的边数减小，而 $G'_1$ 不可能再加上任何边．
若 $G'_1$ 是一个偶图，由于操作 $T:G_1 \Rightarrow G'_1$ 不会改变点的奇偶性，那么 $G_1$ 本身也是个偶图，这与 $G$ 本身是个好图相矛盾．引理2证毕．
回到原题．我们用反证法，假设 $G$ 是一个好图，而所有 $G$ 上的操作 $T$ 都只能将 $G$ 变为一个坏图 $G'$．然后我们分情况推出矛盾．
情况1．若 $T$ 产生了一个 $K_n$．
情况1．1．如图：
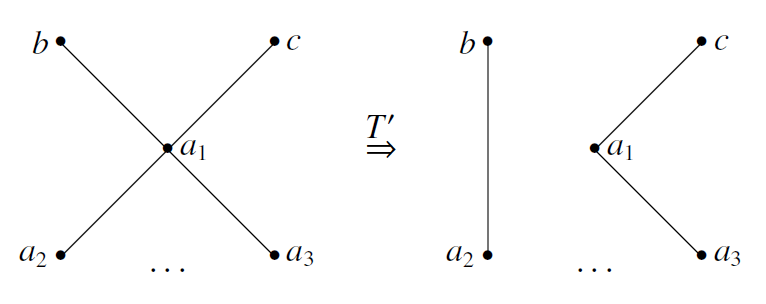在这种情况，由于 $T$ 是撕裂的，它将 $K_n$ 独立出来，则 $a_2 , \ldots , a_n$ 都与 $b,c$ 无边，否则与引理2矛盾，则这是我们考虑 $T'$：此时 $a_1 , a_2$ 无边，$b,c$ 无边，$T'$ 并不会形成一个完全图的连通分支，若新生成的这个分支是一个偶图，则显然原像也是一个偶图，矛盾．故 $T'(G)$ 是一个好图，矛盾．
情况1．2．
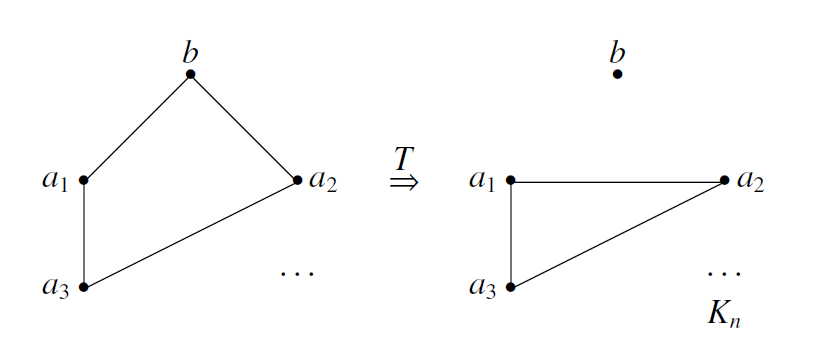若 $n\geqslant 4$，则考虑 $T'$：由 $b$ 与 $a_4$ 无边，则新生成图无完全的连通分支，矛盾．若 $n=3$，则只能是：
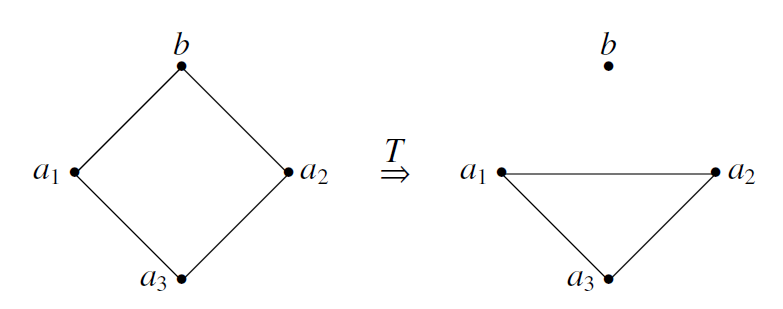若 $b$ 与其他点都不相邻，则 $G$ 本身含有 $(b,a_1 , a_2 , a_3 )$ 这个偶图，矛盾．所以 $b$ 必然与其他点相邻，不妨是 $c$，则我们考虑操作 $T'$：
若这个图是个偶图，则原像也是个偶图，则 $G$ 是坏的，矛盾．所以 $T'(G)$ 是好的，矛盾．
情况2．$T$ 会生成一个 $E_m$（$m\geqslant 4$），
情况2．1．如图：
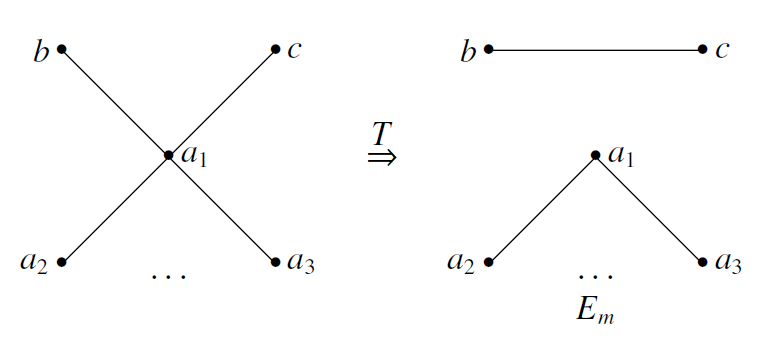则我们考虑另外的操作 $T'$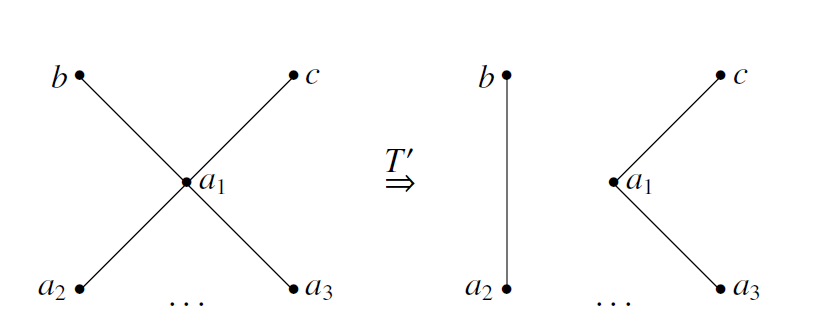：同样的理由知，这个新的图不是偶图，且显然不会是一个完全图，所以 $T'(G)$ 是一个好图，矛盾．情况2．2．如图：
这时我们考虑另外一种操作 $T'$：所以若 $($ 一团 $,b,a_2 , \ldots , a_n )$ 是一个偶图，则原来的 $($ 一团 $,b,a_1,\ldots,a_n )$ 也是一个偶图，矛盾．所以 $T'(G)$ 是一个好图，矛盾．
综上，命题成立．
证法二
用图论的语音来描述这个问题，有一个 $2019$ 阶简单图，其中 $1010$ 个顶点的度为 $1009$，$1009$ 个顶点的度为 $1010$．允许进行如下操作，如果有三个顶点 $A,B,C$ 满足 $AB,AC$ 是边，而 $BC$ 不是边，则可删去边 $AB,AC$，添上边 $BC$．要证明，存在一个操作序列，使得操作结束后，这个图变为若干条不相邻的边，以及一些孤立顶点．
由于 $G$ 中任意两个顶点 $u,v$ 的度之和不小于 $2018$，要么 $u,v$ 相邻，要么 $u,v$ 有公共的邻点，因此 $G$ 是连通的，且 $G$ 显然不是完全图，并且有顶点的度为奇数．事实上．结论对一个连通的非完全图，且有顶点的度为奇数的图都成立．下面仅假设 $G$ 是这样的一个图．
第一步：若 $G$ 不是树，则可通过若干次操作，使得图变为树．注意到操作不改变顶点的度的奇偶性，因此有度为奇数的顶点这一性质始终保持．只需说明若不是树，可通过一次操作使得图仍是连通的，这样由于每次操作减少一条边，必定在有限次操作后该图变为树．
取 $G$ 中的最大圈 $x_1,x_2,\cdots,x_k,x_1$．若这个圈不是哈密顿（Hamilton）圈，则存在一个顶点，不妨设是 $x_1$，它与不在该圈上的某个顶点 $y$ 相邻，于是 $y$ 不与 $x_2$ 相邻，否则就有个更大的圈 $x_1,y,x_2,\cdots,x_k,x_1$．删去边 $x_1y,x_1x_2$ 添上边 $yx_2$ 后，得到的图仍是连通的．
若这个圈是哈密顿圈，由于有奇数度的顶点，因此整个图不能只是这个圈，也不是完全图，因此存在一条弦，不妨设 $x_1x_i$，满足 $x_1,x_{i+1}$ 不相邻，或者 $x_1,x_{i-1}$ 不相邻．不妨设 $x_1,x_{i+1}$ 不相邻，那么可以删去 $x_1x_i,x_ix_{i+1}$，添上边 $x_1x_{i+1}$，得到的图仍是连通的．
第二步：若 $G$ 是树，则可通过若干次操作，使得图变为若干条不相邻的边，以及一些孤立顶点．如果 $G$ 只有一个或两个顶点，结论已经成立．假设 $G$ 至少含有三个顶点，则存在一个顶点 $u$，度至少是 $2$．设 $uv,uw$ 是 $u$ 处的两条边，则 $v,w$ 不相邻，删去边 $uv,uw$（此时变为三个连通分支），再添上边 $vw$，此时图有两个连通分支，并且每个连通分支仍是树．对至少含有三个顶点的连通分支再作同样的操作，直至每个连通分支都含有一个或两个顶点，这便是我们所需的结果．
答案
解析
备注
