2019年第60届IMO试题

• 知识点

  >

  二试几何部分

略

证法一
如图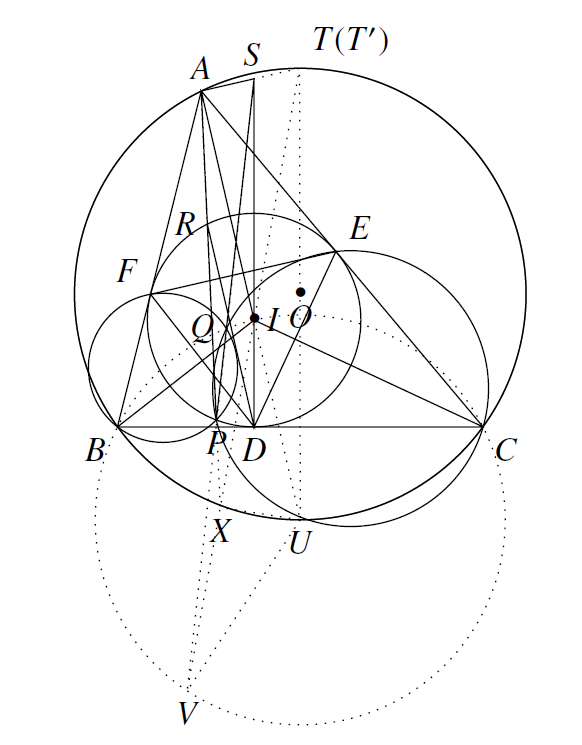记 $PQ$ 与 $DI$ 交于 $S$，记 $\triangle ABC$ 外接圆心为 $O$，延长 $AS,AI$ 交 $\odot O$ 于 $T,U$，延长 $DI$ 交 $\odot I$ 于 $W$．记 $U$ 关于 $\odot O$ 的对径点为 $T'$．
考虑以 $U$ 为圆心，$UB$ 为半径的圆，则由鸡爪定理知 $I,C$ 在 $\odot U$ 上，且 $\angle BQC = \angle BQP + \angle CQP = \angle BFP + \angle CEP = \angle FAP + \angle APF + \angle EAP + \angle APE = \angle BAC + \angle EDF = \angle BIC$，即 $Q$ 也在 $\odot U$ 上．
我们将证明 $T=T'$，于是 $\angle SAI=\angle TAU = 90^{\circ}$．易有 $\angle RFE=\dfrac{1}{2}\angle ABC$，$\angle REF =\dfrac{1}{2}\angle ACB$，则 $
\triangle REF\sim\triangle IBC$ ①
另外，$\angle T'BC = \angle T'AC = 90^{\circ}-\angle CAI = 90^{\circ}-\dfrac{1}{2}\angle BAC = \angle AFE$，所以 $
\triangle AFE \sim \triangle T'BC
$ ②
延长 $T'I$ 交 $\odot U$ 于 $V$，那么由 ①，② 我们易得 $\angle OT'V = \angle OT'I =\angle IAP$．
于是我们延长 $AP$ 交 $T'I$ 于 $X$，则 $A,T',X,U$ 共圆，即 $X$ 在 $\odot O$ 上，故 $UX\perp T'I$，则 $IX=XV$．
由 ①，② 我们易有 $\triangle BVC\sim\triangle FPE$，则 $\angle API = \angle T'VU = \angle UIV$，故 $\angle XIP = \angle IAX$．
由 $P,Q,E,C$ 和 $P,Q,F,B$ 分别共圆有 $\angle PQC = \angle PEC = \angle PFE = \angle VBC =\angle VQC$，即 $S,Q,P,V$ 共线．
设 $AT'$ 交 $DI$ 于 $S'$，记 $\alpha=\angle IUT'=\angle AIS'$，$\beta=\angle IT'O=\angle IAP$．
那么对三角形 $AXT'$ 来说，我们有$$\begin{aligned}
\frac{AS'}{S'T'}&=\frac{AI}{IT'}\cdot\frac{\sin\angle AIS'}{\sin\angle S'IT'}=\frac{AI}{IT'}\cdot\frac{\sin\alpha}{\sin\beta} =\frac{\cos(\alpha+\beta)\sin\alpha}{\sin\beta} \\
\frac{T'V}{VX}&=\frac{T'U}{UX}\cdot\frac{\sin\angle T'UV}{\sin\angle VUX}=\frac{1}{\sin\beta}\cdot\frac{\sin(\angle VT'U+\angle T'VU)}{\cos\angle XVU}=\frac{\sin(2\beta+\alpha)}{\sin\beta\cos(\alpha+\beta)} \\
\frac{PX}{PA}&=\frac{IX}{IA}\cdot\frac{\sin\angle PIX}{\sin\angle PIA}=\frac{IX}{IA}\cdot\frac{\sin\angle PIX}{\sin\angle PIU} = \frac{\sin^2 \beta}{\sin(2\beta+\alpha)\sin\alpha}
\end{aligned}$$故 $\dfrac{AS'}{S'T'}\cdot\dfrac{T'V}{VX}\cdot\dfrac{XP}{PA}=1$，
即 $S',V,P$ 共线．
那么 $S,S'$ 都是 $DI,PQ$ 的交点，所以 $S=S'$，那么 $T=T'$，命题得证．
证法二
如图所示，设 $DI$ 与 $\angle BAC$ 的外角平分线交于点 $L$，于是 $AL\perp AI$．只需再证明 $L,Q,P$ 共线．设 $DL$ 与 $\omega$ 的另一个交点为 $K$，$EF$ 的中点为 $N$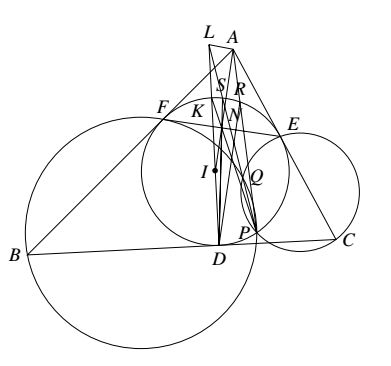．（1）$K,N,P$ 共线，由于 $RFPE$ 是调和四边形，由调和四边形的性质可知 $EF$ 平分 $\angle RNP$．又 $\dfrac{1}{2}\overparen{KF}+\dfrac{1}{2}\overparen{FD}=90^circ=\dfrac{1}{2}\overparen{RE}+\dfrac{1}{2}\overparen{FD}$，故 $\overparen{KF}=\overparen{RE}$，即 $K,R$ 关于 $AI$ 对称，因此 $\angle KNF=\angle RNE=\angle PNE$，故 $K,N,P$ 共线．
（2）$L,S,P$ 共线．由于 $A$ 是 $N$ 关于 $\omega$ 的反演点，$LA\perp AI$，故直线 $AL$ 是 $N$ 关于 $\omega$ 的极线．设 $PS$ 与 $DK$ 交于点 $L^\prime$，则 $L^\prime$ 的极线经过 $N$，$N$ 的极线经过 $L^\prime$，故 $L^\prime$ 在直线 $AL$ 上，于是 $L^\prime=L$，故 $L,S,P$ 共线．
只需证 $S,Q,P$ 共线．如图所示．我们采用有向角的记号，使得角度上的叙述不依赖于特定的图形，用 $\angle(a,b)$ 表示由直线 $a$ 逆时针旋转至直线 $b$ 的方向时所转过的角度，在有向角的等式中，都按模 $\pi$ 理解．由于 $B,F,Q,P$ 共圆，$C,E,Q,P$ 共圆，故
$\begin{aligned}
\angle (BQ,QC)&=\angle (BQ,QP)+\angle (PQ,QC)\\
&=\angle (BF,FP)+\angle (PE,EC)\\
&=\angle (EF,EP)+\angle (FP,FE)\\
&=\angle (FP,EP)\\
&=\angle (DF,DE)=\angle (BI,IC)
\end{aligned}$
从而 $B,I,Q,C$ 共圆．设直线 $QP$ 与 $\odot (BIQC)$ 交于另一点 $T$，直线 $IT$ 与 $DS$ 交于点 $M$．
（3）$M$ 是 $DN$ 的中点．注意到 $\angle (BI,IT)=\angle (BQ,QT)=\angle (BF,FP)=\angle (FK,KP)$．且由 $FD\perp FK,FD\perp BI$，故 $FK\parallel BI$，因此 $IT\parallel KNP$．又 $I$ 是 $DK$ 的中点，因此 $M$ 是 $DN$ 的中点．
现在我们来证明 $S,P,T$ 共线，这将完成整个问题的证明．如图所示．设 $DF,DE$ 的中点分别为 $F_1,E_1$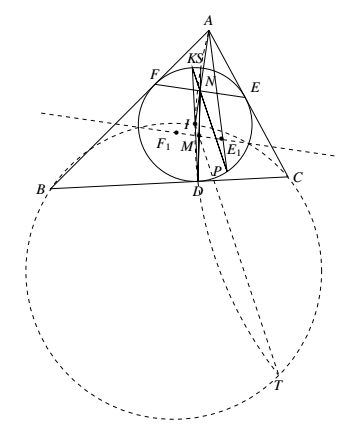．由于 $DF_1\cdot F_1F=DF_1^2=BF_1\cdot F_1I$，故 $F_1$ 在 $\omega$ 与 $\odot(BIC)$ 的根轴上．类似地，$E_1$ 也在 $\omega$ 与 $\odot(BIC)$ 的根轴上，因此直线 $E_1F_1$ 就是 $\omega$ 与 $\odot (BIC)$ 的根轴，由于 $M$ 是 $DN$ 的中点，故 $M$ 在 $E_1F_1$ 上，因此 $M$ 对 $\omega$ 与 $\odot (BIC)$ 等幂．从而 $DM\cdot MS=IM\cdot MT$，这表明 $S,I,D,T$ 共圆．于是
$\angle (DS,ST)=\angle (DI,IT)=\angle (DK,KP)=\angle (DS,SP)$，故 $S,P,T$ 共线．
证法三
如图，在 $\triangle ABC$ 的外接圆 $\Omega$ 上，设 $\overparen{BAC}$ 与 $\overparen{BC}$ 的中点分别为 $M_a,N_a$．设直线 $DL$ 与 $AM_a$ 交于点 $L$．注意到 $AM_a\perp AN_a$ 且 $A,I,N_a$ 三点共线，故 $AL\perp AI$．下面只需证明 $P,Q,L$ 三点共线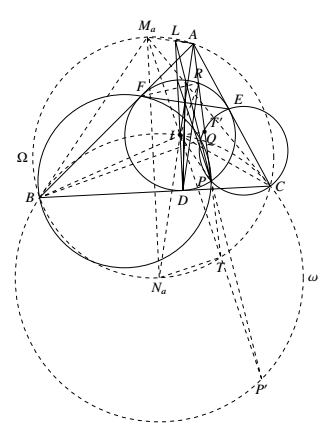．以 $N_a$ 为圆心，$IN_a$ 为半径作圆 $\omega$．由内心的性质可知点 $B,C$ 均在圆 $\omega$ 上．延长 $M_aI$，与圆 $\Omega,\omega$ 分别相交于点 $T,P^\prime$．
（1）凹四边形 $AERF\sim$ 凹四边形 $M_aCIB$．
首先 $AE=AF$ 且 $M_aC=M_aB$，并且 $\angle (FA,AE)=\angle (BA,AC)=\angle (BM_a,M_aC)$，故 $\triangle EAF\sim\triangle CM_aB$．又 $\angle (RE,EF)=\dfrac{\pi}{2}-\angle (DR,RE)=\dfrac{\pi}{2}-\angle (DE,EC)=\angle (IC,CB)$，同理 $\angle (RF,FE)=\angle (IB,BC)$，故凹四边形 $AERF\sim$ 凹四边形 $M_aCIB$．
（2）$A,P,T$ 三点共线．
由（1）可知，在凹四边形 $AERF$ 与 $ACIB$ 中，$\odot I$ 与 $\odot N_a=\omega$ 是对应圆，$AR$ 与 $M_aI$ 是对应直线，所以 $P,P^\prime$ 也是对应点．于是 $\angle (PA,AE)=\angle (P^\prime M_a,M_aC)=\angle (TM_a,M_aC)=\angle (TA,AC)$，因此 $A,P,T$ 三点共线．
（3）$P,Q,P^\prime$ 三点共线．由 $B,P,Q,F$ 四点共圆及弦切角定理可知 $\angle (BQ,QP)=\angle (BF,FP)=\angle (FR,RP)$，同理 $\angle (PQ,QC)=\angle (PR,RE)$，因此
$\begin{aligned}
\angle (BQ,QC)&=\angle (BQ,QP)+\angle (PQ,QC)\\
&=\angle (FR,RP)+\angle (PR,RE)\\
&=\angle (FR,RE)=\angle (BI,IC)
\end{aligned}$
故 $B,I,Q,C$ 四点共圆，即点 $Q$ 在圆 $\omega$ 上．于是
$\begin{aligned}
\angle (BQ,QP^\prime)&=\angle (BI,IP^\prime)+\angle (BI,IM_a)\\
&=\angle (FR,RA)=\angle (FR,RP)\\
&=\angle (BF,FP)=\angle (BQ,QP)
\end{aligned}$
故 $P,Q,P^\prime$ 三点共线．
（4）$P,Q,L$ 三点共线．在 $\triangle AM_aL$ 中，只需证明 $\dfrac{AP}{PT}\cdot\dfrac{TP^\prime}{P^\prime M_a}\cdot\dfrac{M_aL}{LA}=1$．
过点 $I$ 作 $PR$ 的垂线，垂足是 $T^\prime$．注意到 $N_aT\perp IP^\prime$，故在凹四边形 $AERF$ 与 $M_aCIB$ 中，$T^\prime$ 与 $T$ 是对应点．因此 $\dfrac{TP^\prime}{P^\prime M_a}=\dfrac{T^\prime P}{PA}$．
在直角三角形 $ITT^\prime$ 与 $M_aAN_a$ 中，有 $\angle (T^\prime T,TI)=\angle (AT,TM_a)=\angle (AN_a,N_aM_a)$，所以 $\triangle ITT^\prime\sim\triangle M_aN_aA$．又结合凹四边形 $AERF\sim$ 凹四边形 $M_aCIB$ 可知 $\angle (IP,PT)=\angle (AR,RI)=\angle (M_aI,IN_a)$，所以 $P,I$ 是相似三角形 $ITT^\prime$ 与 $M_aN_aA$ 的对应点．结合 $IL\parallel M_aN_a$ 可知 $\dfrac{M_aL}{LA}=\dfrac{N_aI}{IA}=\dfrac{TP}{PT^\prime}$．
于是 $\dfrac{AP}{PT}\cdot\dfrac{TP^\prime}{P^\prime M_a}\cdot\dfrac{M_aL}{LA}=\dfrac{AP}{PT}\cdot\dfrac{T^\prime P}{PA}\cdot\dfrac{TP}{PT^\prime}=1$．
由梅涅劳斯定理的逆定理可知 $P,Q,L$ 三点共线．
综上可知结论成立．
证法四
如图，设 $\triangle ABC$ 的外接圆中，$\overparen{BC}$（不含 $A$）的中点为 $N$，$\overparen{BAC}$ 的中点为 $L$．以 $N$ 为圆心，$IN$ 为半径作圆，记之为 $\odot N$，则 $\odot N$ 过点 $B,C$．设 $LI$ 的延长线交 $\odot N$ 于点 $U$，交 $\triangle ABC$ 的外接圆于点 $S$．设 $\triangle AFE$ 的外接圆（记为 $\Omega$）与 $\triangle ABC$ 的外接圆（记为 $\Omega$）交于点 $A$ 与 $M$．设 $DI,AL$ 交于点 $V$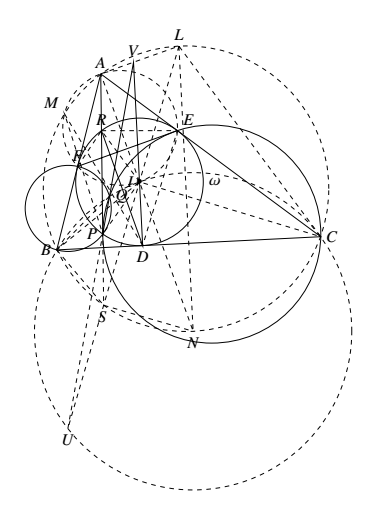．下面依次证明：
（1）$A,R,S$ 三点共线．令 $\angle BAC=2\alpha,\angle ABC=2\beta,\angle ACB=2\gamma$．
注意到 $\angle BSI=\angle ISC$，且
$\begin{aligned}
\angle IBS&=\angle IBC+\angle SBC=\beta+\angle CLI=\gamma+(\beta-\gamma)+\angle CLI\\
&=\angle ICA+\angle LCA+\angle CLI=\angle CIS
\end{aligned}$
故 $\triangle IBS\sim\triangle CIS$．于是有
$\dfrac{\sin\angle BAS}{\sin\angle CAS}=\dfrac{BS}{CS}=\dfrac{BS}{IS}\cdot\dfrac{IS}{CS}=\left(\dfrac{BI}{IC}\right)^2=\left(\dfrac{\sin\gamma}{\sin\beta}\right)^2$．
由 $I$ 为 $\omega$ 的圆心，$DR\perp EF$，知 $\angle EDR=\angle FDI=\beta,\angle FDR=\angle EDI=\gamma$，故 $\dfrac{\sin\angle BAR}{\sin\angle CAR}=\dfrac{\angle AFR}{\sin\angle RFE}\cdot\dfrac{\sin\angle REF}{\sin\angle REA}=\left(\dfrac{\sin\angle FDR}{\sin\angle EDR}\right)^2=\left(\dfrac{\sin\gamma}{\sin\beta}\right)^2=\dfrac{\sin\angle BAS}{\sin\angle CAS}.$
故 $A,R,S$ 三点共线．（1）证毕．
（2）$U,P,Q$ 三点共线．因为 $\angle AFE=\angle AEF=\angle LBC=\angle LCB=90^\circ-\alpha$，有 $\triangle AFE$ 与 $\triangle LBC$ 旋转相似，而 $M$ 在它们的外接圆 $\Omega_1$ 和 $\Omega$ 上，故 $M$ 为 $\Omega_1$ 和 $\Omega$ 的旋转相似中心．
由于 $AI,LN$ 分别为 $\Omega_1$ 和 $\Omega$ 的直径，故 $I,N$ 为相似对应点，进而 $\omega$ 和 $\odot N$ 为相似对应圆．而 $\angle FAR=\angle BAS=\angle BLS$，故 $AR,LS$ 为相似对应直线，于是 $AR$ 与 $\omega$ 的交点 $R,P$ 的相似对应点分别为 $LS$ 与 $\odot N$ 的交点 $I,U$．
因此有 $\angle BIU=\angle FRP=\angle BFP=\angle BQP$．而由
$\begin{aligned}
\angle BQC&=\angle BAC+\angle ABQ+\angle ACQ=\angle BAC+\angle FPQ+\angle EPQ\\
&=\angle BAC+\angle FPE=2\alpha+\angle FDE=90^\circ+\alpha=\angle BIC
\end{aligned}$
知 $Q$ 在 $\odot N$ 上，故 $\angle BQU=\angle BIU=\angle BQP$，即 $U,P,Q$ 三点共线．（2）证毕．
（3）$A,M,P,V$ 四点共圆．由（2）中 $\triangle AFE$ 与 $\triangle LBC$ 的旋转相似关系（$M$ 为旋转相似中心），知 $\triangle MFB\sim\triangle MEC$，故 $\dfrac{MB}{MC}=\dfrac{EB}{EC}=\dfrac{BD}{CD}$，故 $MD$ 平分 $\angle BMC$，从而 $M,D,N$ 三点共线．
以下由 $DV\parallel LN$ 知 $\angle MDV=\angle MDL=180^\circ-\angle MAV$，有 $A,M,D,V$ 四点共圆．
又由 $RD\perp EF,AN\perp EF$ 知 $RD\parallel AN$，故 $\angle PAN=\angle PRD=\angle PDB$，而 $\angle MAN=\angle MAB+\alpha=\angle MCB+\angle CMN=\angle MDB$，故 $\angle MAP=\angle MAN-\angle PAN=\angle MDB-\angle PDB=\angle MDP$，得 $A,M,P,D$ 四点共圆．
所以 $A,M,P,D,V$ 五点共圆．（3）证毕．
（4）$U,V,P,Q$ 四点共线．
由（3）知 $\angle MPV=180^\circ-\angle MAV=90^\circ-\angle MAN=\angle MIA=\angle MFA$．
在（2）的旋转相似关系中，点 $M,F,P$ 分别对应点 $M,B,U$，故有 $\angle MPU=\angle MFB=180^\circ-\angle MFA=180^\circ-\angle MPV$，即 $U,V,P$ 三点共线．结合（2）知 $U,V,P,Q$ 四点共线．（4）证毕．
由（4）知原命题获证．
证法五
如图，设 $DI$ 与 $\angle BAC$ 的外角平分线交于点 $L$，则 $AL\perp AI$，只需再证明 $L,P,Q$ 三点共线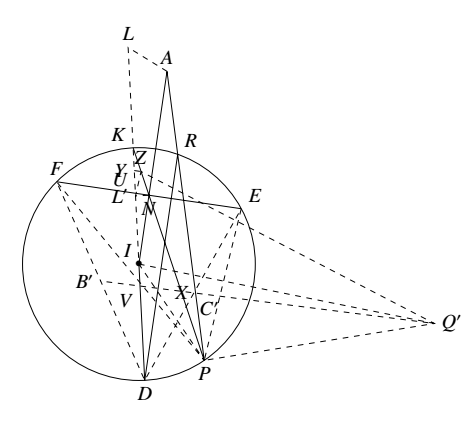．考虑以 $\odot I$ 为基圆的反演变换，设点 $A,B,C,\cdots$ 的反演像分别为 $A^\prime,B^\prime,C^\prime,\cdots$ 以此类推．不难知道 $\odot I$ 上点的反演像是本身，而 $B^\prime,C^\prime$ 分别是 $DF,ED$ 的中点．设 $EF$ 的中点是 $N$，过 $N$ 作直线 $DI$ 的垂线，则垂足恰为 $L^\prime$．欲证 $L,P,Q$ 三点共线，只需证 $I,L^\prime,P,Q^\prime$ 四点共圆．
设 $DI$ 的延长线与 $\odot I$ 交于点 $K$，$EF,B^\prime C^\prime$ 分别与 $DK$ 交于点 $U,V$，直线 $B^\prime C^\prime,PK$ 交于点 $X$．设线段 $KU,KN$ 的中点分别是 $Y,Z$．
（1）$P,N,K$ 三点共线．由于 $KR\perp DR$ 且 $DR\perp EF$，故 $KR\parallel EF$．于是 $\overparen{FK}=\overparen{ER}$，即 $\angle FPK=\angle EPR$．注意到四边形 $ERFP$ 是调和四边形，由调和四边形的性质知 $N$ 在线段 $PK$ 上．
（2）$Q^\prime$ 在直线 $B^\prime C^\prime$ 上．由于 $P,B,F,Q$ 四点共圆且 $P,C,E,Q$ 四点共圆，结合反演变换的性质可知 $P,B^\prime,F,Q^\prime$ 四点共圆且 $P,C^\prime,E,Q^\prime$ 四点共圆．于是
$\angle (B^\prime Q^\prime,Q^\prime P)=\angle (B^\prime F,FP)=\angle (DF,FP)=\angle (DE,EP)=\angle (C^\prime E,EP)=\angle (C^\prime Q^\prime ,Q^\prime P)$，因此 $Q^\prime$ 在直线 $B^\prime C^\prime $ 上．
（3）$P,Q^\prime ,K,V$ 四点共圆且 $\triangle PQ^\prime X\sim \triangle VKX$．由 $P,B^\prime,F,Q^\prime $ 四点共圆可知
$\begin{aligned}
\angle (VQ^\prime,Q^\prime P)&=\angle (B^\prime Q^\prime,Q^\prime P)=\angle (B^\prime F,FP)\\
&=\angle (DF,FP)=\angle (DK,KP)=\angle (VK,KP)
\end{aligned}$
故 $P,Q^\prime,K,V$ 四点共圆，进而 $\triangle PQ^\prime X\sim\triangle VKX$．
（4）$\triangle PIQ^\prime\sim\triangle XZQ^\prime$ 且 $P,I,Z,Q^\prime$ 四点共圆．由于
$\begin{aligned}
\angle (PK,PI)&=\angle (IK,KP)=\angle (DK,KP)=\angle (DE,EP)\\
&=\angle (C^\prime E,EP)=\angle (C^\prime Q^\prime,Q^\prime P)
\end{aligned}$
故
$\begin{aligned}
\angle (Q^\prime P,PI)&=\angle (Q^\prime P,PK)+\angle (PK,PI)\\
&=\angle (Q^\prime P,PK)+\angle (C^\prime Q^\prime,Q^\prime P)\\
&=\angle (C^\prime Q^\prime,PK)\\
&=\angle (Q^\prime X,XZ)
\end{aligned}$
注意到 $V$ 是线段 $DU$ 的中点，所以
$\overrightarrow{VY}=\overrightarrow{VU}+\overrightarrow{UY}=\dfrac{1}{2}\overrightarrow{DU}+\dfrac{1}{2}\overrightarrow{UK}=\dfrac{1}{2}\overrightarrow{DK}$，
故 $VY=\dfrac{1}{2}DK=IP$．结合 $YZ\parallel UN\parallel VX$ 及 $\triangle PQ^\prime X\sim\triangle VKX$ 可得 $\dfrac{IP}{ZX}=\dfrac{VY}{ZX}=\dfrac{KV}{KX}=\dfrac{Q^\prime P}{Q^\prime X}$，于是 $\triangle PIQ^\prime\sim\triangle XZQ^\prime$．
因此 $\angle (PI,IQ^\prime)=\angle (XZ,ZQ^\prime)=\angle (PZ,ZQ^\prime)$，进而 $P,I,Z,Q^\prime$ 四点共圆．
（5）$P,I,L^\prime ,Z$ 四点共圆．由 $KL^\prime\perp L^\prime N$ 与 $KZ=ZN$ 可知
$\begin{aligned}
\angle (L^\prime Z,ZP)&=\angle (L^\prime Z,ZN)=2\angle (L^\prime K,KN)\\
&=2\angle (DK,KP)=\angle (LI^\prime ,IP)
\end{aligned}$
因此 $P,I,L^\prime ,Z$ 四点共圆．
结合（4）与（5）可知 $I,L^\prime,Z,Q^\prime,P$ 五点共圆．由反演的性质知 $L,P,Q$ 三点共线，命题证毕．
证法六
如图，设 $DI$ 与 $\angle BAC$ 的外角平分线交于点 $L$，则 $AL\perp AI$，只需再证明 $L,P,Q$ 三点共线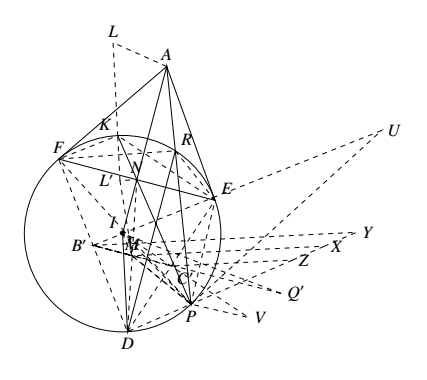．考虑以 $\odot I$ 为基圆的反演变换，设点 $A,B,C,\cdots$ 的反演分别为 $A^\prime,B^\prime,C^\prime,\cdots$ 以此类推．不难知道 $\odot I$ 上点的反演像是本身，而 $B^\prime,C^\prime$ 分别是 $DF,DE$ 的中点．设 $EF$ 的中点是 $N$，过 $N$ 作直线 $DI$ 的垂线，则垂足恰为 $L^\prime$．欲证 $L,P,Q$ 三点共线，只需证 $I,L\prime,,P,Q^\prime$ 四点共圆．
设 $DI$ 的延长线于 $\odot I$ 交于点 $K$．记过 $P,B^\prime,F$ 三点的圆是 $\Gamma_1$，过 $P,C^\prime,E$ 三点的圆是 $\Gamma_2$．由反演的性质知 $Q^\prime$ 是圆 $\Gamma_1,\Gamma_2$ 除点 $P$ 以外的另一个交点．记过 $I,P,L^\prime$ 三点的圆是 $\gamma$，则只需证明圆 $\Gamma_1,\Gamma_2,\gamma$ 共轴．
引理：（开世圆幂定理）设 $\Gamma_1,\Gamma_2$ 是平面上的两圆．用 $p(T,\Gamma_i)$ 表示点 $T$ 对圆 $\Gamma_i$ 的幂，$i=1,2$．设实数 $\lambda\ne 0,1$，则满足 $\dfrac{p(T,\Gamma_1)}{p(T,\Gamma_2)}=\lambda$ 的点 $T$ 构成的轨迹是与 $\Gamma_1,\Gamma_2$ 共轴的圆．
引理证明：设圆 $\Gamma_1,\Gamma_2$ 的标准方程（形如 $x^2+y^2+dx+ey+f=0$ 的方程）分别是 $F_1(x,y)=0$ 与 $F_2(x,y)=0$，则点 $P$ 的轨迹方程是 $F_1-\lambda F_2=0$．
因为 $\lambda\ne 1$，故这是圆的方程，其标准方程是 $\dfrac{F_1-\lambda F_2}{1-\lambda}=F_1\Leftrightarrow F_1-F_2=0$，这与圆 $\Gamma_1,\Gamma_2$ 的根轴相同，引理证毕．
回到原题，设 $B^\prime C^\prime ,DN$ 交于点 $M$，圆 $\Gamma_1,\Gamma_2,\gamma$ 分别与直线 $DP$ 相交于除 $P$ 以外的另一点 $Y,Z,X$．设 $FU,EV$ 分别是圆 $\Gamma_1,\Gamma_2$ 的直径．
（1）$P,N,K$ 三点共线．由于 $\triangle AER\sim\triangle APE,\triangle AFR\sim\triangle APF$，所以 $\dfrac{ER}{PE}=\dfrac{AE}{AP}=\dfrac{AF}{AP}=\dfrac{FR}{PF}$，即 $ER\cdot PF=FR\cdot PE$．又结合 $DR\perp EF$ 可知 $\angle (KD,DF)=\dfrac{\pi}{2}-\angle (FE,ED)=\angle (ED,DR)$，故 $ER=FK,FR=EK$．因此 $FK\cdot PF=EK\cdot PE$．结合 $\angle (PF,FK)=\angle (PE,ER)$ 及面积正弦定理可知 $S_{\triangle PFK}=S_{\triangle PEK}$，因此 $P,N,K$ 三点共线．
（2）$M$ 在圆 $\gamma$ 上且 $MX\perp DK$．注意到 $M$ 是 $DN$ 的中点且 $DL^\prime\perp NL^\prime$，故 $\angle (IL^\prime ,L^\prime M)=\angle (IP,PM)$．
于是 $\angle (IL^\prime ,L^\prime M)=\angle (IP,PM)$，即 $I,M,P,L^\prime$ 四点共圆．因此 $M$ 在圆 $\gamma$ 上，进而
$\angle (MX,XP)=\angle (MI,IP)=\angle (KP,PI)=\angle (DK,KP).$
注意到 $XP\perp KP$，所以 $MX\perp DK$．
（3）$B^\prime Y\perp DK,C^\prime Z\perp DK$，并且 $\dfrac{p(X,\Gamma_1)}{p(X,\Gamma_2)}=-1$．由 $B^\prime ,P,F,Y$ 四点共圆可知 $\angle (B^\prime Y,YP)=\angle (B^\prime F,FP)=\angle (DF,FP)=\angle (DK,KP)$．
注意到 $YP\perp KP$，所以 $B^\prime P\perp DK$．同理 $C^\prime Z\perp DK$．结合（2）可知 $MX\parallel B^\prime Y\parallel C^\prime Z$．又 $M$ 是 $B^\prime C^\prime$ 的中点，所以 $X$ 也是 $YZ$ 的中点．于是 $\dfrac{p(X,\Gamma_1)}{p(X,\Gamma_2)}=\dfrac{\overline{XP}\cdot\overline{XY}}{\overline{XP}\cdot\overline{XZ}}=-1$．
（4）$\dfrac{p(I,\Gamma_1)}{p(I,\Gamma_2)}=-1$．注意到 $FB^\prime \perp B^\prime U$ 且 $FB^\prime \perp B^\prime I$，所以 $B^\prime ,I,U$ 三点共线．同理 $C^\prime ,I,V$ 三点共线．结合 $VP\perp PE$ 且 $UP\perp PF$，有 $\angle (IU,UP)=\angle (DF,FP)=\angle (DE,EP)=\angle (IV,VP)$，进而 $I,P,U,V$ 四点共圆．于是
$\dfrac{IU}{IV}=\dfrac{\sin\angle (UP,PI)}{\sin\angle (VP,PI)}=\dfrac{\cos\angle (PF,PI)}{\cos\angle (EP,PI)}=\dfrac{PF}{PE}$．
结合（1）的结论就有 $\dfrac{IU}{IV}=\dfrac{PF}{PE}=\dfrac{KE}{KF}=\dfrac{IC^\prime}{IB^\prime}$，即 $IB^\prime \cdot IU=IC^\prime \cdot IV$．因此 $\dfrac{p(I,\Gamma_1)}{p(I,\Gamma_2)}=\dfrac{\overline{IB^\prime}\cdot\overline{IU}}{\overline{IC^\prime}\cdot\overline{IV}}=-1$．
由（3）与（4）可知圆 $\gamma$ 与 $\Gamma_1,\Gamma_2$ 共根轴．又 $Q^\prime$ 是 $\Gamma_1,\Gamma_2$ 的公共点，所以 $Q^\prime$ 也在圆 $\gamma$ 上，进而 $I,L^\prime ,P,Q^\prime$ 四点共圆，命题证毕．