在矩形 $ABCD$ 中，点 $M,N,P,Q$ 分别在边 $AB,BC,CD,DA$ 上，使得 $S_{\triangle AQM}=S_{\triangle BMN}=S_{\triangle CNP}=S_{\triangle DPQ}$．
证明：四边形 $MNPQ$ 为平行四边形．
证明：四边形 $MNPQ$ 为平行四边形．
【难度】
【出处】
2015年第二届伊朗几何奥林匹克
【标注】
【答案】
略
【解析】
如图，设 $AB= CD= a, AD =BC=b,AM=x, PC= y, AQ = z, NC=t$．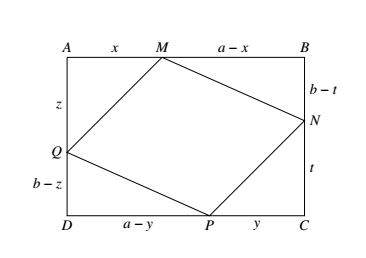
若 $x\ne y$，不妨设 $x>y$，则 $a-x<a-y$ ①
由 $S_{\triangle AQM}=S_{\triangle CNP}\Rightarrow xz=yt\Rightarrow z<t\Rightarrow b-t<b-z$．②
由式 ①② 得
$\dfrac{1}{2}(a-x)(b-t)<\dfrac{1}{2}(a-y)(b-z)\Rightarrow S_{\triangle BMN}<S_{\triangle DPQ}$，这与题设矛盾．因此，$x=y$．
类似可证 $z=t$．
于是，$\triangle AMQ\cong \triangle CPN\Rightarrow MQ=PN$．
类似可证 $MN=PQ$．
从而，四边形 $MNPQ$ 为平行四边形．
若 $x\ne y$，不妨设 $x>y$，则 $a-x<a-y$ ①由 $S_{\triangle AQM}=S_{\triangle CNP}\Rightarrow xz=yt\Rightarrow z<t\Rightarrow b-t<b-z$．②
由式 ①② 得
$\dfrac{1}{2}(a-x)(b-t)<\dfrac{1}{2}(a-y)(b-z)\Rightarrow S_{\triangle BMN}<S_{\triangle DPQ}$，这与题设矛盾．因此，$x=y$．
类似可证 $z=t$．
于是，$\triangle AMQ\cong \triangle CPN\Rightarrow MQ=PN$．
类似可证 $MN=PQ$．
从而，四边形 $MNPQ$ 为平行四边形．
答案
解析
备注
