如图,点 $P,A,B$ 在圆上,点 $Q$ 在圆的内部,使得 $\angle PAQ=90^\circ$,且 $PQ=BQ$.证明:$\angle AQB-\angle PQA=\overparen{AB}^\circ$.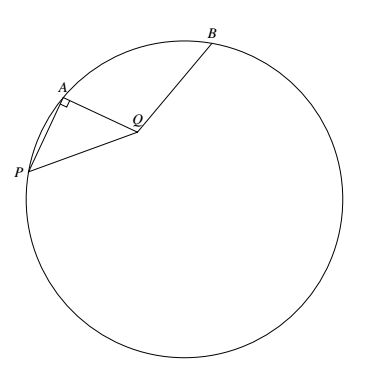

【难度】
【出处】
2015年第二届伊朗几何奥林匹克
【标注】
【答案】
略
【解析】
设 $M$ 为 $PB$ 的中点.则 $\angle PMQ=90^\circ$.又 $\angle PAQ=90^\circ$,于是,$A、P、Q、M$ 四点共圆
$\begin{aligned}
&\Rightarrow \angle APM=\angle AQM\\
& \angle AQB-\angle PQA=\angle PQM+\angle AQM-\angle PQA \\
& =2\angle AQM=2\angle APB=\overparen{AB}^\circ
\end{aligned}$.
$\begin{aligned}
&\Rightarrow \angle APM=\angle AQM\\
& \angle AQB-\angle PQA=\angle PQM+\angle AQM-\angle PQA \\
& =2\angle AQM=2\angle APB=\overparen{AB}^\circ
\end{aligned}$.
答案
解析
备注