设正 $\triangle ABC$ 的外接圆为 $\odot O$，$P$ 为弧 $\overparen{BC}$ 上一点，过点 $P$ 作 $\odot O$ 的切线，分别与 $AB、AC$ 的延长线交于点 $K、L$．证明：$\angle KOL>90^\circ$．
【难度】
【出处】
2015年第二届伊朗几何奥林匹克
【标注】
【答案】
略
【解析】
如图，设 $M、N$ 分别为 $AB、AC$ 的中点．则 $B、M、N、C$ 四点共圆．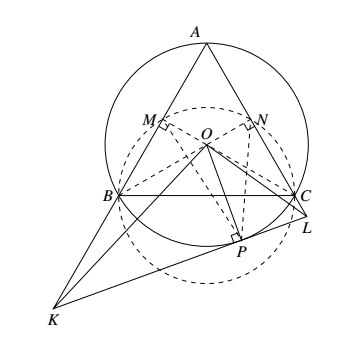
因为 $\angle BPC = 120^\circ>90^\circ$，所以，点 $P$ 在 $B,M,N,C$ 四点所共圆的内部．
因此，$\angle MPN>\angle MBN=30^\circ$．
又 $K,M,O,P,L,N,O,P$ 均四点共圆，故
$\begin{aligned}
&\angle MKO=\angle MPO,\angle NLO=\angle NPO\\
&\Rightarrow \angle AKO+\angle ALO=\angle MPN>30^\circ\\
&\Rightarrow \angle KOL=\angle A+\angle AKO+\angle ALO>90^\circ
\end{aligned}$
因为 $\angle BPC = 120^\circ>90^\circ$，所以，点 $P$ 在 $B,M,N,C$ 四点所共圆的内部．因此，$\angle MPN>\angle MBN=30^\circ$．
又 $K,M,O,P,L,N,O,P$ 均四点共圆，故
$\begin{aligned}
&\angle MKO=\angle MPO,\angle NLO=\angle NPO\\
&\Rightarrow \angle AKO+\angle ALO=\angle MPN>30^\circ\\
&\Rightarrow \angle KOL=\angle A+\angle AKO+\angle ALO>90^\circ
\end{aligned}$
答案
解析
备注
