如图,在 $\triangle ABC$ 中,$AC>AB$,圆 $\mathit{\Gamma}$ 为 $\triangle ABC$ 的外接圆.设 $X$ 为线段 $AC$ 上一点,$Y$ 为圆 $\mathit{\Gamma}$ 上一点(点 $A,Y$ 在直线 $BC$ 的异侧),满足 $CX=CY=AB$,直线 $XY$ 与圆 $\mathit{\Gamma}$ 的另一个交点为 $P$.证明:$PB=PC$.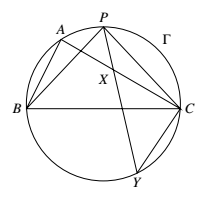

【难度】
【出处】
2016年第三届伊朗几何奥林匹克
【标注】
【答案】
略
【解析】
因为 $CX=CY$,所以,$\angle YXC=\angle XYC$.
这表明,$\overparen{AP}+\overparen{CY}=\overparen{PC}$.
又 $AB=CY$,则
$\begin{aligned}
&\overparen{AB}=\overparen{CY}\\
&\Rightarrow \overparen{AP}+\overparen{CY}=\overparen{AP}+\overparen{AB}=\overparen{PB}\\
&\Rightarrow\overparen{PB}=\overparen{PC}\Rightarrow PB=PC.
\end{aligned}$
这表明,$\overparen{AP}+\overparen{CY}=\overparen{PC}$.
又 $AB=CY$,则
$\begin{aligned}
&\overparen{AB}=\overparen{CY}\\
&\Rightarrow \overparen{AP}+\overparen{CY}=\overparen{AP}+\overparen{AB}=\overparen{PB}\\
&\Rightarrow\overparen{PB}=\overparen{PC}\Rightarrow PB=PC.
\end{aligned}$
答案
解析
备注