在 $Rt \triangle ABC$ 中，$\angle BAC=90^\circ$，边 $BC$ 上的垂直平分线与 $AC$ 交于点 $K$，线段 $BK$ 的垂直平分线与 $AB$ 交于点 $L$．若 $CL$ 平 $\angle ACB$，求 $\angle ABC,\angle ACB$ 的所有可能值．
【难度】
【出处】
2016年第三届伊朗几何奥林匹克
【标注】
【答案】
略
【解析】
分三种情形考虑．
（1）$ AC >AB$．
如图，设 $\angle LBK=\angle LKB=\alpha$．
则 $\angle KLA=2\alpha,\angle LKA=90^\circ-\angle KLA=90^\circ-2\alpha$．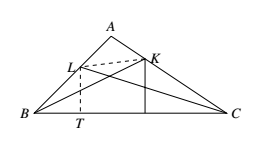
由 $BK=KC\Rightarrow \angle KBC=\angle KCB=\dfrac{1}{2}\angle BKA=\dfrac{1}{2}((90^\circ-\alpha)+2\alpha)=45^\circ+\dfrac{1}{2}\alpha$．
作 $LT\perp BC$，垂足为 $T$．
因为 $CL$ 平分 $\angle ACB$，所以，$LT=LA$．
又 $LB=LK,\angle BTL=\angle KAL=90^\circ$
$\begin{aligned}
&\Rightarrow \triangle BTL\cong \triangle KAL\\
&\Rightarrow \angle LBT=\angle LKA\\
&\Rightarrow\alpha+\left(45^\circ-\dfrac{\alpha}{2}\right)=90^\circ-2\alpha\\
&\Rightarrow\alpha=18^\circ\\
&\Rightarrow\angle ABC=45^\circ+\dfrac{1}{2}\alpha=54^\circ\\
&\Rightarrow\angle ACB=90^\circ-\angle ABC=36^\circ
\end{aligned}$
（2）$AC<AB$．
如图，设 $\angle LBK=\angle LKB=\alpha$．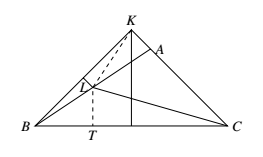
则 $\angle KLA=2\alpha,\angle LKA=90^\circ-\angle KLA=90^\circ-2\alpha$．
作 $LT\perp BC$，垂足为 $T$．
因为 $CL$ 平分 $\angle ACB$，所以，$LT=LA$．
由 $LB=LK,\angle BTL=\angle KAL=90^\circ$
$\begin{aligned}
&\Rightarrow \triangle BTL\cong \triangle KAL\\
&\Rightarrow \angle LBT=\angle LKA=90^\circ -2\alpha\\
&\Rightarrow \angle CKB=\angle CBK=90^\circ-\alpha\\
&\Rightarrow CB=CK
\end{aligned}$
又 $BK=CK$，则 $\triangle BKC$ 为等边三角形．
故 $\angle CBK=90^\circ-\alpha=60^\circ\Rightarrow \alpha=30^\circ\Rightarrow \angle ABC=90^\circ-2\alpha=30^\circ,\angle ACB=\angle KCB=60^\circ$．
（3）$AC=AB$．
此时，点 $K$ 与 $A$ 重合，$L$ 即边 $AB$ 的中点．于是，$CL$ 即为 $\triangle ABC$ 的中线又为 $\triangle ABC$ 的角平分线，这是不可能的．
（1）$ AC >AB$．
如图，设 $\angle LBK=\angle LKB=\alpha$．
则 $\angle KLA=2\alpha,\angle LKA=90^\circ-\angle KLA=90^\circ-2\alpha$．
由 $BK=KC\Rightarrow \angle KBC=\angle KCB=\dfrac{1}{2}\angle BKA=\dfrac{1}{2}((90^\circ-\alpha)+2\alpha)=45^\circ+\dfrac{1}{2}\alpha$．作 $LT\perp BC$，垂足为 $T$．
因为 $CL$ 平分 $\angle ACB$，所以，$LT=LA$．
又 $LB=LK,\angle BTL=\angle KAL=90^\circ$
$\begin{aligned}
&\Rightarrow \triangle BTL\cong \triangle KAL\\
&\Rightarrow \angle LBT=\angle LKA\\
&\Rightarrow\alpha+\left(45^\circ-\dfrac{\alpha}{2}\right)=90^\circ-2\alpha\\
&\Rightarrow\alpha=18^\circ\\
&\Rightarrow\angle ABC=45^\circ+\dfrac{1}{2}\alpha=54^\circ\\
&\Rightarrow\angle ACB=90^\circ-\angle ABC=36^\circ
\end{aligned}$
（2）$AC<AB$．
如图，设 $\angle LBK=\angle LKB=\alpha$．
则 $\angle KLA=2\alpha,\angle LKA=90^\circ-\angle KLA=90^\circ-2\alpha$．作 $LT\perp BC$，垂足为 $T$．
因为 $CL$ 平分 $\angle ACB$，所以，$LT=LA$．
由 $LB=LK,\angle BTL=\angle KAL=90^\circ$
$\begin{aligned}
&\Rightarrow \triangle BTL\cong \triangle KAL\\
&\Rightarrow \angle LBT=\angle LKA=90^\circ -2\alpha\\
&\Rightarrow \angle CKB=\angle CBK=90^\circ-\alpha\\
&\Rightarrow CB=CK
\end{aligned}$
又 $BK=CK$，则 $\triangle BKC$ 为等边三角形．
故 $\angle CBK=90^\circ-\alpha=60^\circ\Rightarrow \alpha=30^\circ\Rightarrow \angle ABC=90^\circ-2\alpha=30^\circ,\angle ACB=\angle KCB=60^\circ$．
（3）$AC=AB$．
此时，点 $K$ 与 $A$ 重合，$L$ 即边 $AB$ 的中点．于是，$CL$ 即为 $\triangle ABC$ 的中线又为 $\triangle ABC$ 的角平分线，这是不可能的．
答案
解析
备注
