如图,圆 $\Gamma_1,\Gamma_2$ 交于 $A,B$ 两点.圆 $\Gamma_1$,在点 $A$ 处的切线与圆 $\Gamma_2$ 的另一个交点为 $P$,直线 $PB$ 与圆 $\Gamma_1$ 的另一个交点为 $Q$,过 $Q$ 作圆 $\Gamma_2$ 的切线,与圆 $\Gamma_1,\Gamma_2$ 分别交于 $C、D$ 两点(点 $A,D$ 在直线 $PQ$ 的异侧).证明:$AD$ 平分 $\angle CAP$.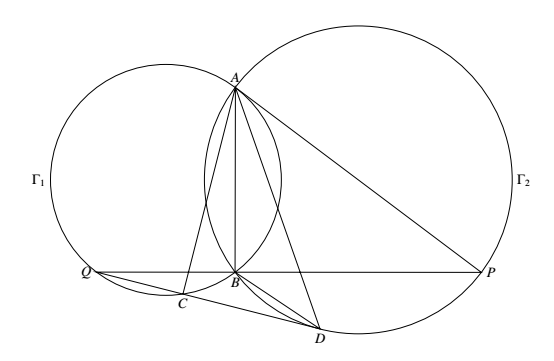

【难度】
【出处】
2016年第三届伊朗几何奥林匹克
【标注】
【答案】
略
【解析】
由圆周角定理知 $\angle CAB=\angle CQB$.再由弦切角定理得 $\angle DAB=\angle BDQ$.则 $\angle CAD=\angle CAB+\angle DAB=\angle CQB+\angle BDQ=\angle PBD=\angle PAD$.因此,$AD$ 平分 $\angle CAP$.
答案
解析
备注