在 $Rt\triangle ABC$ 中，$\angle BAC=90^\circ,\triangle ABC$ 的外接圆 $\Gamma$ 在点 $A$ 处的切线与 $BC$ 交于点 $P$，$M$ 为劣弧 $\overparen{AB}$ 的中点，线段 $PM$ 与圆 $\Gamma$ 的另一个交点为 $Q$，圆 $\Gamma$ 在点 $Q$ 处的切线与 $AC$ 交于点 $K$．证明：$\angle PKC=90^\circ$．
【难度】
【出处】
2016年第三届伊朗几何奥林匹克
【标注】
【答案】
略
【解析】
首先假设 $AB<AC$．如图．
由 $\triangle PMA\sim\triangle PAQ\Rightarrow \dfrac{AQ}{MA}=\dfrac{PQ}{PA}$．
由 $\triangle PMB\sim\triangle PCQ\Rightarrow \dfrac{MB}{QC}=\dfrac{PB}{PQ}$．
结合 $MA=MB$，将上述两式相乘得 $\dfrac{AQ}{QC}=\dfrac{PB}{PA}$．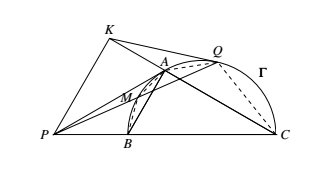
由 $\triangle PBA\sim\triangle PAC\Rightarrow \dfrac{AC}{BA}=\dfrac{PA}{PB}\Rightarrow \dfrac{AQ}{QC}=\dfrac{BA}{AC}$ ①
由 $\triangle KAQ\sim\triangle KQC\Rightarrow \dfrac{KA}{KQ}=\dfrac{KQ}{KC}\Rightarrow \dfrac{AQ}{QC}=\dfrac{KA}{KC}=\left(\dfrac{AQ}{QC}\right)^2$ ②
由 $\triangle PBA\sim\triangle PAC\Rightarrow \dfrac{PB}{PA}=\dfrac{PA}{PC}=\dfrac{BA}{AC}\Rightarrow \dfrac{PB}{PC}=\left(\dfrac{BA}{AC}\right)^2$ ③
结合 ①②③ 得 $\dfrac{KA}{KC}=\dfrac{PB}{PC}$．
于是，$PK\parallel AB$．从而，$\angle PKC=90^\circ$．
当 $AB>AC$ 时，证明方法相同．
由 $\triangle PMA\sim\triangle PAQ\Rightarrow \dfrac{AQ}{MA}=\dfrac{PQ}{PA}$．
由 $\triangle PMB\sim\triangle PCQ\Rightarrow \dfrac{MB}{QC}=\dfrac{PB}{PQ}$．
结合 $MA=MB$，将上述两式相乘得 $\dfrac{AQ}{QC}=\dfrac{PB}{PA}$．
由 $\triangle PBA\sim\triangle PAC\Rightarrow \dfrac{AC}{BA}=\dfrac{PA}{PB}\Rightarrow \dfrac{AQ}{QC}=\dfrac{BA}{AC}$ ①由 $\triangle KAQ\sim\triangle KQC\Rightarrow \dfrac{KA}{KQ}=\dfrac{KQ}{KC}\Rightarrow \dfrac{AQ}{QC}=\dfrac{KA}{KC}=\left(\dfrac{AQ}{QC}\right)^2$ ②
由 $\triangle PBA\sim\triangle PAC\Rightarrow \dfrac{PB}{PA}=\dfrac{PA}{PC}=\dfrac{BA}{AC}\Rightarrow \dfrac{PB}{PC}=\left(\dfrac{BA}{AC}\right)^2$ ③
结合 ①②③ 得 $\dfrac{KA}{KC}=\dfrac{PB}{PC}$．
于是，$PK\parallel AB$．从而，$\angle PKC=90^\circ$．
当 $AB>AC$ 时，证明方法相同．
答案
解析
备注
