已知圆 $\Gamma,\Gamma^\prime$ 交于 $A,B$ 两点.圆 $\Gamma$ 在点 $A$ 处的切线与圆 $\Gamma^\prime$ 的另一个交点为 $C$,圆 $\Gamma^\prime$ 在点 $A$ 处的切线与 $\Gamma$ 的另一个交点为 $D$.设 $\angle CAD$ 的内角平分线与圆 $\Gamma,\Gamma^\prime$ 分别交于 $E,F$ 两点,$\angle CAD$ 的外角平分线与圆 $\Gamma,\Gamma^\prime$ 分别交于点 $X,Y$.证明:线段 $XY$ 的垂直平分线与 $\triangle BEF$ 的外接圆相切.
【难度】
【出处】
2016年第三届伊朗几何奥林匹克
【标注】
【答案】
略
【解析】
如图,设直线 $XE$ 与 $FY$ 交于点 $P$.
结合已知条件和弦切角定理,设 $\angle EXA=\angle EAC=\angle EAD=\angle FYA= \alpha$.于是,$PX=PY$.由 $\angle ABE=\angle AXE=\alpha,\angle ABF= 180^\circ -\angle AYF= 180^\circ-\alpha$,知 $\angle EBF=\angle ABF-\angle ABE=(180^\circ-\alpha)-\alpha=180^\circ-2\alpha$.
显然,$\angle EPF=2\alpha$.
从而,$P,E,B,F$ 四点共圆.
又 $\angle PEF=\angle AEX=90^\circ-\alpha=\angle AFY\Rightarrow PE=PF$.
因此,$P$ 为 $\triangle BEF$ 的外接圆上的弧 $\overparen{EF}$ 的中点.
而线段 $XY$ 的垂直平分线平行于 $EF$ 且通过点 $P$,故线段 $XY$ 的垂直平分线与 $\triangle BEF$ 的外接圆切于点 $P$.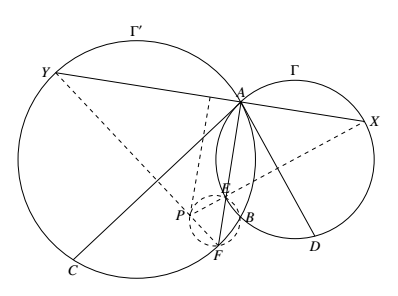
结合已知条件和弦切角定理,设 $\angle EXA=\angle EAC=\angle EAD=\angle FYA= \alpha$.于是,$PX=PY$.由 $\angle ABE=\angle AXE=\alpha,\angle ABF= 180^\circ -\angle AYF= 180^\circ-\alpha$,知 $\angle EBF=\angle ABF-\angle ABE=(180^\circ-\alpha)-\alpha=180^\circ-2\alpha$.
显然,$\angle EPF=2\alpha$.
从而,$P,E,B,F$ 四点共圆.
又 $\angle PEF=\angle AEX=90^\circ-\alpha=\angle AFY\Rightarrow PE=PF$.
因此,$P$ 为 $\triangle BEF$ 的外接圆上的弧 $\overparen{EF}$ 的中点.
而线段 $XY$ 的垂直平分线平行于 $EF$ 且通过点 $P$,故线段 $XY$ 的垂直平分线与 $\triangle BEF$ 的外接圆切于点 $P$.

答案
解析
备注