已知凸四边形 $ABC$ D的边 $AD,BC$ 所在直线交于点 $P$．设 $I_1,I_2$ 分别为 $\triangle PAB$ 内切圆，$\triangle PDC$ 内切圆的圆心，$O$ 为 $\triangle PAB$ 外接圆的圆心，$H$ 为 $\triangle PDC$ 的垂心．证明：$\triangle AI_1B$ 的外接圆与 $\triangle DHC$ 的外接圆相切，当且仅当 $\triangle AOB$ 的外接圆与 $\triangle DI_2C$ 的外接圆相切．
【难度】
【出处】
2016年第三届伊朗几何奥林匹克
【标注】
【答案】
略
【解析】
如图，设 $\triangle AI_1B$ 的外接圆与 $\triangle DHC$ 的外接圆切于点 $K,Q$ 为 $\triangle AKD $ 的外接圆与 $\triangle BKC$ 的外接圆的另一个交点．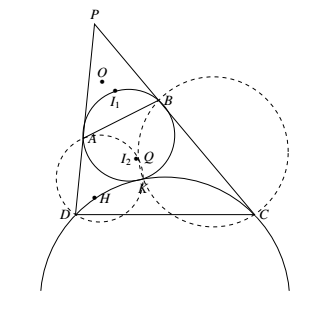
则 $\angle DHC=\angle DKC= 180^\circ -\angle P$．
注意到，$\angle PDK+\angle PCK=\angle DKC-\angle P=180^\circ-2\angle P$．
由 $A、Q、K、D$ 四点共圆知 $\angle AQK= 180^\circ-\angle PDK$；
由 $B、Q、K、C$ 四点共圆知 $\angle BQK= 180^\circ-\angle PCK$．
故
$\begin{aligned}
&\angle AQB=360^\circ -\angle AQK-\angle BQK\\
&=\angle PDK+\angle PCK=180^\circ-2\angle P\\
&=180^\circ-\angle AOB
\end{aligned}$
于是，$A、O、B、Q$ 四点共圆．
又 $\angle AKD=\angle AQD,\angle BKC=\angle BQC,\angle AQB=\angle DKC-\angle P$，
则 $\angle C Q D$
$=360^{\circ}-\angle A Q D-\angle B Q C-\angle A Q B$
$=\angle A K B+\angle P$
$=180^{\circ}-\angle A I_{1} B+\angle P=90^{\circ}+\dfrac{\angle P}{2}$
$=\angle D I_{2} C$
从而，$C、D、Q、I_2$ 四点共圆
由 $\triangle AI_1B$ 的外接圆与 $\triangle DHC$ 的外接圆切于点 $K$，知
$\angle A B K+\angle D C K=\angle A K D\Rightarrow(\angle A B Q+\angle K B Q)+(\angle D C Q-\angle K C Q)=\angle A K D$
又 $\angle K B Q=\angle K C Q, \angle A K D=\angle A Q D\Rightarrow \angle A B Q+\angle D C Q=\angle A Q D$
因此，$\triangle AOB$ 的外接圆与 $\triangle DI_2C$ 的外接圆切于点 $Q$．
反之，假设 $\triangle CI_2D$ 的外接圆与 $\triangle AOB$ 的外接圆切于点 $Q$，$K$ 为 $\triangle AQD$ 的外接圆与 $\triangle BQC$ 的外接圆的另一个交点．
类似地，$\triangle AI_1B$ 的外接圆与 $\triangle DHC$ 的外接圆切于点 $K$．
则 $\angle DHC=\angle DKC= 180^\circ -\angle P$．注意到，$\angle PDK+\angle PCK=\angle DKC-\angle P=180^\circ-2\angle P$．
由 $A、Q、K、D$ 四点共圆知 $\angle AQK= 180^\circ-\angle PDK$；
由 $B、Q、K、C$ 四点共圆知 $\angle BQK= 180^\circ-\angle PCK$．
故
$\begin{aligned}
&\angle AQB=360^\circ -\angle AQK-\angle BQK\\
&=\angle PDK+\angle PCK=180^\circ-2\angle P\\
&=180^\circ-\angle AOB
\end{aligned}$
于是，$A、O、B、Q$ 四点共圆．
又 $\angle AKD=\angle AQD,\angle BKC=\angle BQC,\angle AQB=\angle DKC-\angle P$，
则 $\angle C Q D$
$=360^{\circ}-\angle A Q D-\angle B Q C-\angle A Q B$
$=\angle A K B+\angle P$
$=180^{\circ}-\angle A I_{1} B+\angle P=90^{\circ}+\dfrac{\angle P}{2}$
$=\angle D I_{2} C$
从而，$C、D、Q、I_2$ 四点共圆
由 $\triangle AI_1B$ 的外接圆与 $\triangle DHC$ 的外接圆切于点 $K$，知
$\angle A B K+\angle D C K=\angle A K D\Rightarrow(\angle A B Q+\angle K B Q)+(\angle D C Q-\angle K C Q)=\angle A K D$
又 $\angle K B Q=\angle K C Q, \angle A K D=\angle A Q D\Rightarrow \angle A B Q+\angle D C Q=\angle A Q D$
因此，$\triangle AOB$ 的外接圆与 $\triangle DI_2C$ 的外接圆切于点 $Q$．
反之，假设 $\triangle CI_2D$ 的外接圆与 $\triangle AOB$ 的外接圆切于点 $Q$，$K$ 为 $\triangle AQD$ 的外接圆与 $\triangle BQC$ 的外接圆的另一个交点．
类似地，$\triangle AI_1B$ 的外接圆与 $\triangle DHC$ 的外接圆切于点 $K$．
答案
解析
备注
