在凸四边形 $ABCD$ 中，边 $AB、CD$ 所在直线交于点 $E$，边 $AD、BC$ 所在直线交于点 $F$，对角线 $AC$ 与 $BD$ 交于点 $P$．过点 $D$ 的圆 $\Gamma_1$ 与 $AC$ 切于点 $P$，过点 $C$ 的圆 $\Gamma_2$ 与 $BD$ 切于点 $P$．$AD$ 与圆 $\Gamma_1$ 交于点 $X$，$BC$ 与圆 $\Gamma_2$ 交于点 $P$．设圆 $\Gamma_1,\Gamma_2$ 交于除点 $P$ 外的另一点 $Q$．证明：过点 $P$ 且垂直于 $EF $ 的直线通过 $\triangle XQY$ 外接圆的圆心．
【难度】
【出处】
2016年第三届伊朗几何奥林匹克
【标注】
【答案】
略
【解析】
设 $\triangle XQY$ 的外接圆圆心为 $O$．以 $P$ 为反演中心关于某个圆作反演变换，得到的图形如图．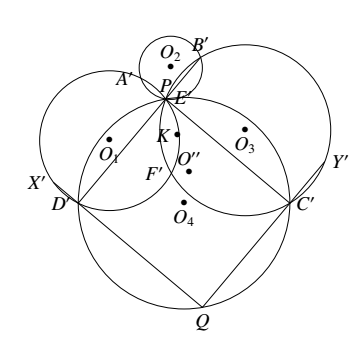
于是，点 $X^\prime$ 为点 $X$ 在反演变换下的像，其余的类似．
接下来证明：$PO^\prime$ 为 $\triangle E^\prime PF^\prime$ 的外接圆的直径．
设 $O^{\prime\prime}$ 为 $\triangle X^\prime Q^\prime Y^\prime$ 的外接圆圆心．
于是，$P、O^{\prime}、O^{\prime\prime}$ 三点共线．
下面只需证明 $PO^{\prime\prime}$ 通过么 $\triangle E^\prime PF^\prime$ 的外接圆圆心．
设 $O_1、O_2、O_3、O_4$ 为图中四个圆的圆心，$K$ 为 $O_1O_3$ 与 $O_2O_4$ 的交点．
由 $ K$ 为线段 $PE^\prime、PF^\prime$ 的垂直平分线的交点，知 $K$ 为 $\triangle PE^\prime F^\prime$ 的外接圆圆心
又四边形 $D^\prime B^\prime Y^\prime Q^\prime$ 为等腰梯形，故点 $O^{\prime\prime}$ 在线段 $B^\prime D^\prime$ 的垂直平分线上．
类似地，点 $O^{\prime\prime}$ 也在线段 $A^\prime C^\prime$ 的垂直平分线上．
假设 $A^\prime C^\prime$ 分别与 $O_1O_2、O_3O_4$ 交于点 $M、T$，$B^\prime D^\prime$ 分别与 $O_2O_3、O_1O_4$ 交于点 $N、L$．过点 $ K、O^{\prime\prime}$ 作 $A^\prime C^\prime$ 的垂线，垂足分别为 $U、V$；过点 $K、O^{\prime\prime}$ 作 $B^\prime D^\prime$ 的垂线，垂足分别为 $R、S$．
由 $O_1O_2\perp A^\prime C^\prime ,O_3O_4\perp A^\prime C^\prime\Rightarrow O_1O_2\parallel O_3O_4$．
类似地 $O_2O_3\parallel O_1O_4$．
于是，四边形 $O_1O_2O_3O_4$ 为平行四边形．这表明，$K$ 为线段 $O_1O_3、O_2O_4$ 的中点．
因此，$UM=UT$．
又 $A^\prime M=PM,C^\prime T=PT$，则
$P V=A^{\prime} V-A^{\prime} P=(P M+P T)-2 P M=P T-P M$
$ \Rightarrow T V=P T-P V=P M \Rightarrow U P=U V$
类似地，$RP=RS$．
因此，点 $K$ 在线段 $PV、PS$ 的垂直平分线上，即 $K$ 为 $\triangle PSV$ 的外接圆圆心．
从而，$P,K,O^{\prime\prime}$ 三点共线．
于是，点 $X^\prime$ 为点 $X$ 在反演变换下的像，其余的类似．接下来证明：$PO^\prime$ 为 $\triangle E^\prime PF^\prime$ 的外接圆的直径．
设 $O^{\prime\prime}$ 为 $\triangle X^\prime Q^\prime Y^\prime$ 的外接圆圆心．
于是，$P、O^{\prime}、O^{\prime\prime}$ 三点共线．
下面只需证明 $PO^{\prime\prime}$ 通过么 $\triangle E^\prime PF^\prime$ 的外接圆圆心．
设 $O_1、O_2、O_3、O_4$ 为图中四个圆的圆心，$K$ 为 $O_1O_3$ 与 $O_2O_4$ 的交点．
由 $ K$ 为线段 $PE^\prime、PF^\prime$ 的垂直平分线的交点，知 $K$ 为 $\triangle PE^\prime F^\prime$ 的外接圆圆心
又四边形 $D^\prime B^\prime Y^\prime Q^\prime$ 为等腰梯形，故点 $O^{\prime\prime}$ 在线段 $B^\prime D^\prime$ 的垂直平分线上．
类似地，点 $O^{\prime\prime}$ 也在线段 $A^\prime C^\prime$ 的垂直平分线上．
假设 $A^\prime C^\prime$ 分别与 $O_1O_2、O_3O_4$ 交于点 $M、T$，$B^\prime D^\prime$ 分别与 $O_2O_3、O_1O_4$ 交于点 $N、L$．过点 $ K、O^{\prime\prime}$ 作 $A^\prime C^\prime$ 的垂线，垂足分别为 $U、V$；过点 $K、O^{\prime\prime}$ 作 $B^\prime D^\prime$ 的垂线，垂足分别为 $R、S$．
由 $O_1O_2\perp A^\prime C^\prime ,O_3O_4\perp A^\prime C^\prime\Rightarrow O_1O_2\parallel O_3O_4$．
类似地 $O_2O_3\parallel O_1O_4$．
于是，四边形 $O_1O_2O_3O_4$ 为平行四边形．这表明，$K$ 为线段 $O_1O_3、O_2O_4$ 的中点．
因此，$UM=UT$．
又 $A^\prime M=PM,C^\prime T=PT$，则
$P V=A^{\prime} V-A^{\prime} P=(P M+P T)-2 P M=P T-P M$
$ \Rightarrow T V=P T-P V=P M \Rightarrow U P=U V$
类似地，$RP=RS$．
因此，点 $K$ 在线段 $PV、PS$ 的垂直平分线上，即 $K$ 为 $\triangle PSV$ 的外接圆圆心．
从而，$P,K,O^{\prime\prime}$ 三点共线．
答案
解析
备注
