如图,菱形 $EFGH$ 内接于 $\triangle ABC$,且 $AF = EF = CG = EB$.求 $\angle ABC$ 的值.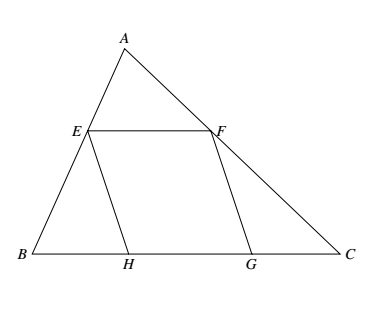

【难度】
【出处】
2017年第四届伊朗几何奥林匹克
【标注】
【答案】
略
【解析】
由题意知
$\angle AFE=\angle CFC=\angle C,\angle B=\angle EHB=\angle FGH=2\angle C$.在等腰 $\triangle AEF$ 中,$\angle A=\angle AEF= \dfrac{1}{2} (180^\circ -\angle C)=90^\circ -\dfrac{1}{2}\angle C$.
由 $\angle A+\angle B+\angle C= 180^\circ\Rightarrow \left(90^\circ-\dfrac{1}{2} \angle C\right)+ 2 \angle C + \angle C = 180^\circ\Rightarrow \angle C=36^\circ$.
故 $\angle ABC=72^\circ$.
$\angle AFE=\angle CFC=\angle C,\angle B=\angle EHB=\angle FGH=2\angle C$.在等腰 $\triangle AEF$ 中,$\angle A=\angle AEF= \dfrac{1}{2} (180^\circ -\angle C)=90^\circ -\dfrac{1}{2}\angle C$.
由 $\angle A+\angle B+\angle C= 180^\circ\Rightarrow \left(90^\circ-\dfrac{1}{2} \angle C\right)+ 2 \angle C + \angle C = 180^\circ\Rightarrow \angle C=36^\circ$.
故 $\angle ABC=72^\circ$.
答案
解析
备注