在正五边形 $ABCDE$ 中，过点 $C$ 作 $CD$ 的垂线，与边 $AB$ 交于点 $F$．证明：$AE+AF=BE$．
【难度】
【出处】
2017年第四届伊朗几何奥林匹克
【标注】
【答案】
略
【解析】
如图，设直线 $AE$ 与 $FC$ 交于点 $P$．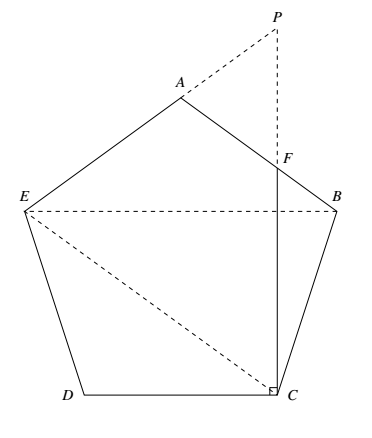
易知，$\angle ECD=36^\circ$．
则 $\angle ECP=54^\circ, \angle AEC=72^\circ\Rightarrow \angle P=54^\circ\Rightarrow CE=PE$．
又 $\angle ECB=\angle EBC=72^\circ$，于是，$BE=CE=PE$．
因为 $\angle EAB=108^\circ$，所以，$\angle AFP=\angle EAB-\angle P=108^\circ-54^\circ=54^\circ=\angle P\Rightarrow AF=AP$．
故 $AE+AF=AE+AP=PE=CE=BE$．
易知，$\angle ECD=36^\circ$．则 $\angle ECP=54^\circ, \angle AEC=72^\circ\Rightarrow \angle P=54^\circ\Rightarrow CE=PE$．
又 $\angle ECB=\angle EBC=72^\circ$，于是，$BE=CE=PE$．
因为 $\angle EAB=108^\circ$，所以，$\angle AFP=\angle EAB-\angle P=108^\circ-54^\circ=54^\circ=\angle P\Rightarrow AF=AP$．
故 $AE+AF=AE+AP=PE=CE=BE$．
答案
解析
备注
