在等腰 $\triangle ABC$ 中，$AB=AC$，$l$ 为过点 $A$ 且平行于边 $BC$ 的直线．设 $D$ 为直线 $l$ 上任意一点，过点 $A$ 作直线 $BD、CD$ 的垂线，垂足分别为 $E、F$，点 $E、F$ 在直线 $l$ 上的射影分别为 $P、Q$．证明：$AP+AQ \leqslant AB$．
【难度】
【出处】
2017年第四届伊朗几何奥林匹克
【标注】
【答案】
略
【解析】
如图，设 $P^\prime、E^\prime$ 分别为点 $P、E$ 关于 $BC$ 垂直平分线的对称点．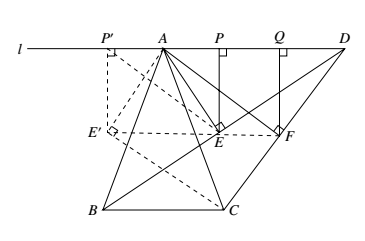
则 $\angle AE^\prime C=\angle APE =90^\circ$ 且 $AP^\prime=AP$．
注意到，$A、E^\prime、C、F$ 四点共圆，且 $AC$ 为该圆的一条直径．
故 $AP+AQ =AP^\prime+AQ = QP^\prime\leqslant FE^\prime\leqslant AC=AB$．
则 $\angle AE^\prime C=\angle APE =90^\circ$ 且 $AP^\prime=AP$．注意到，$A、E^\prime、C、F$ 四点共圆，且 $AC$ 为该圆的一条直径．
故 $AP+AQ =AP^\prime+AQ = QP^\prime\leqslant FE^\prime\leqslant AC=AB$．
答案
解析
备注
