在 $\triangle ABC$ 中，$X、Y$ 为边 $BC$ 上的两点（点 $X$ 在 $B、Y$ 之间），满足 $2XY=BC$，$AA^\prime$ 为 $\triangle AXY$ 外接圆的直径，过点 $B$ 作 $BC$ 的垂线，与直线 $AX$ 交于点 $P$，过点 $C$ 作 $BC$ 的垂线，与直线 $AY$ 交与点 $Q$．证明：$\triangle AXY$ 的外接圆在点 $A^\prime$ 处的切线通过 $\triangle APQ$ 的外心．
【难度】
【出处】
2017年第四届伊朗几何奥林匹克
【标注】
【答案】
略
【解析】
如图，设 $O$ 为 $\triangle APQ$ 的外心，$M、N$ 分别为线段 $AP、AQ$ 的中点．
事实上，只需证 $\angle OA^\prime A= 90^\circ$．设 $H、K、M^\prime、N^\prime$ 分别为点 $A,A^\prime,M,N$ 在边 $BC$ 上的射影．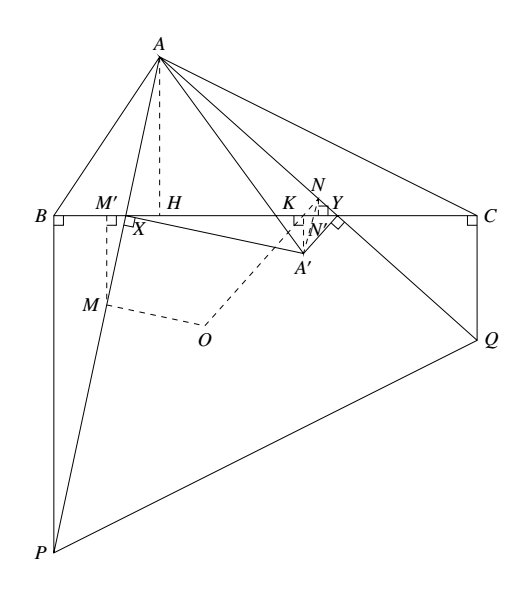
由条件，知 $M、N $ 分别为线段 $AP、AQ$ 的中点．
于是，$BM^\prime=HM^\prime,CN^\prime=HN^\prime$．
则 $XM^\prime=HM^\prime-XH=\dfrac{1}{2}BH-XH$ ①
$YN^\prime=HY-HN^\prime=HY-\dfrac{1}{2}CH=(XY-XH)-\dfrac{BC-BH}{2}\Rightarrow(XY-XH)-\dfrac{BC-BH}{2}\\
\Rightarrow YN^\prime=(XY-\dfrac{1}{2}BC)+(\dfrac{1}{2}BH-XH)=\dfrac{1}{2}BH-XH ② $
结合 ①② 知 $XM^\prime=YN^\prime$．
由 $\angle A^\prime YA=\angle A^\prime XA=90^\circ\Rightarrow \angle KA^\prime Y=\angle NYN^\prime$
$\angle KA^\prime X=\angle MXM^\prime\Rightarrow \triangle A^{\prime} K X \sim \triangle X M^{\prime} M \triangle A^{\prime} K Y \sim \triangle Y N^{\prime} N\Rightarrow \dfrac{A^{\prime} X}{M X}=\dfrac{A^{\prime} K}{X M^{\prime}}, \dfrac{A^{\prime} K}{N Y^{\prime}}=\dfrac{A^{\prime} Y}{N Y}$
两式相除得 $\dfrac{A^\prime X}{MX}=\dfrac{A^\prime Y}{AY}$．
从而，$\triangle A^\prime NY\sim \triangle A^\prime MX$．
因此，$\angle A^\prime MX=\angle A^\prime NY,$ 即 $A,M,A^\prime,N$ 四点共圆．
又 $\angle AMO=\angle ANO=90^\circ$，则 $A,M,O,N$ 也四点共圆．
故 $A、M、O、A^\prime、N$ 五点共圆于以 $AO$ 为直径的圆．
因此，$\angle OA^\prime A=90^\circ$．
事实上，只需证 $\angle OA^\prime A= 90^\circ$．设 $H、K、M^\prime、N^\prime$ 分别为点 $A,A^\prime,M,N$ 在边 $BC$ 上的射影．
由条件，知 $M、N $ 分别为线段 $AP、AQ$ 的中点．于是，$BM^\prime=HM^\prime,CN^\prime=HN^\prime$．
则 $XM^\prime=HM^\prime-XH=\dfrac{1}{2}BH-XH$ ①
$YN^\prime=HY-HN^\prime=HY-\dfrac{1}{2}CH=(XY-XH)-\dfrac{BC-BH}{2}\Rightarrow(XY-XH)-\dfrac{BC-BH}{2}\\
\Rightarrow YN^\prime=(XY-\dfrac{1}{2}BC)+(\dfrac{1}{2}BH-XH)=\dfrac{1}{2}BH-XH ② $
结合 ①② 知 $XM^\prime=YN^\prime$．
由 $\angle A^\prime YA=\angle A^\prime XA=90^\circ\Rightarrow \angle KA^\prime Y=\angle NYN^\prime$
$\angle KA^\prime X=\angle MXM^\prime\Rightarrow \triangle A^{\prime} K X \sim \triangle X M^{\prime} M \triangle A^{\prime} K Y \sim \triangle Y N^{\prime} N\Rightarrow \dfrac{A^{\prime} X}{M X}=\dfrac{A^{\prime} K}{X M^{\prime}}, \dfrac{A^{\prime} K}{N Y^{\prime}}=\dfrac{A^{\prime} Y}{N Y}$
两式相除得 $\dfrac{A^\prime X}{MX}=\dfrac{A^\prime Y}{AY}$．
从而，$\triangle A^\prime NY\sim \triangle A^\prime MX$．
因此，$\angle A^\prime MX=\angle A^\prime NY,$ 即 $A,M,A^\prime,N$ 四点共圆．
又 $\angle AMO=\angle ANO=90^\circ$，则 $A,M,O,N$ 也四点共圆．
故 $A、M、O、A^\prime、N$ 五点共圆于以 $AO$ 为直径的圆．
因此，$\angle OA^\prime A=90^\circ$．
答案
解析
备注
