在 $\triangle ABC$ 中，内切圆 $\odot I$ 与边 $BC$ 切于点 $D$，直线 $DI$ 与边 $AC$ 交于点 $X$，过点 $X$ 作 $\odot I$ 的切线（不同于直线 $AC$）与 $AB$ 交于点 $ Y $，$ Z $ 为 $ YI $ 与 $ BC $ 的交点．证明：$ AB =BZ$．
【难度】
【出处】
2017年第四届伊朗几何奥林匹克
【标注】
【答案】
略
【解析】
如图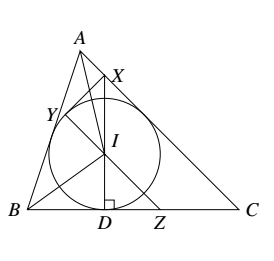
因为 $l$ 为 $\triangle AXY$ 中 $\angle A$ 内的旁心，所以，$\angle XIY=90^\circ-\dfrac{1}{2}-\angle BAC$．
则 $angle IZB=90^\circ -\angle DIZ=90^\circ-\angle XIY=\dfrac{1}{2}\angle BAC\Rightarrow \angle IZB=\angle IAB$．
又 $\angle IBZ =\angle IBA,IB=IB$，知 $\triangle ABI\cong \triangle ZBI \Rightarrow AB =BZ$．
因为 $l$ 为 $\triangle AXY$ 中 $\angle A$ 内的旁心，所以，$\angle XIY=90^\circ-\dfrac{1}{2}-\angle BAC$．则 $angle IZB=90^\circ -\angle DIZ=90^\circ-\angle XIY=\dfrac{1}{2}\angle BAC\Rightarrow \angle IZB=\angle IAB$．
又 $\angle IBZ =\angle IBA,IB=IB$，知 $\triangle ABI\cong \triangle ZBI \Rightarrow AB =BZ$．
答案
解析
备注
