已知 $O$ 为 $\triangle ABC$ 的外心，直线 $CO$ 与边 $BC$ 上的高交于点 $K$，$P、M$ 分别为 $AK、AC$ 的中点，$PO$ 与 $BC$ 交于点 $Y$，$\triangle BCM$ 的外接圆与 $AB$ 交于点 $X$（不与点 $B$ 重合）．证明：$B、X、O、Y$ 四点共圆．
【难度】
【出处】
2017年第四届伊朗几何奥林匹克
【标注】
【答案】
略
【解析】
如图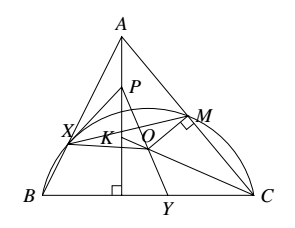
只需证明 $\angle XOP=\angle ABC$．
因为 $\angle ABC=\angle XMA$，所以，$\angle XMO=90^\circ-\angle XMA=90^\circ-\angle ABC=\angle XAK$．
由 $B,X,M,C$ 四点共圆 $\Rightarrow\triangle AXM\sim\triangle ACB\Rightarrow\dfrac{AX}{XM}=\dfrac{AC}{BC}$．
由 $O$ 为 $\triangle ABC$ 的外心 $\Rightarrow\angle OCA=90^\circ-\angle ABC,\angle AKC=180^\circ-\angle BAC$．
在 $\triangle AKC,Rt\triangle OMC$ 中，分别由正弦定理，三角比的定义得 $\dfrac{AC}{\sin\angle BAC}=\dfrac{AK}{\sin(90^\circ-\angle ABC)},OC=\dfrac{OM}{\sin(90^\circ-\angle ABC)}$．
两式相除得 $\dfrac{AK}{OM}=\dfrac{AC}{OC\sin\angle BAC}$．
又 $P$ 为 $AK$ 的中点，则 $\dfrac{AP}{OM}=\dfrac{AC}{2OC\sin\angle ABC}=\dfrac{AC}{BC}$．
故 $\triangle XPA\sim\triangle XOM\Rightarrow\triangle XOP\sim\triangle XMA\Rightarrow \angle XOP=\angle XMA=\angle ABC$．
只需证明 $\angle XOP=\angle ABC$．因为 $\angle ABC=\angle XMA$，所以，$\angle XMO=90^\circ-\angle XMA=90^\circ-\angle ABC=\angle XAK$．
由 $B,X,M,C$ 四点共圆 $\Rightarrow\triangle AXM\sim\triangle ACB\Rightarrow\dfrac{AX}{XM}=\dfrac{AC}{BC}$．
由 $O$ 为 $\triangle ABC$ 的外心 $\Rightarrow\angle OCA=90^\circ-\angle ABC,\angle AKC=180^\circ-\angle BAC$．
在 $\triangle AKC,Rt\triangle OMC$ 中，分别由正弦定理，三角比的定义得 $\dfrac{AC}{\sin\angle BAC}=\dfrac{AK}{\sin(90^\circ-\angle ABC)},OC=\dfrac{OM}{\sin(90^\circ-\angle ABC)}$．
两式相除得 $\dfrac{AK}{OM}=\dfrac{AC}{OC\sin\angle BAC}$．
又 $P$ 为 $AK$ 的中点，则 $\dfrac{AP}{OM}=\dfrac{AC}{2OC\sin\angle ABC}=\dfrac{AC}{BC}$．
故 $\triangle XPA\sim\triangle XOM\Rightarrow\triangle XOP\sim\triangle XMA\Rightarrow \angle XOP=\angle XMA=\angle ABC$．
答案
解析
备注
