在 $\triangle ABC$ 中，$\angle A=60^\circ$，点 $ M、N、K$ 分别在边 $BC、AC、AB$ 上，使得 $BK=KM=MN= NC$．若 $AN=2AK$，求 $\angle B,\angle C$ 的度数．
【难度】
【出处】
2015年第二届伊朗几何奥林匹克
【标注】
【答案】
略
【解析】
如图，取 $AN$ 的中点 $P$．则 $AK= AP = PN$．于是，$\triangle APK$ 为等边三角形．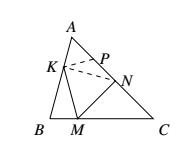
故 $\angle ANK=\dfrac{1}{2}\angle KPA=30^\circ$．
设 $\angle ACB=\angle NMC=\alpha$．则 $\angle ABC=\angle KMB=120^\circ-\alpha$．
所以，$\angle KMN=60^\circ$，即 $\triangle KMN$ 为等边三角形．
于是，$\angle ANM=90^\circ,\alpha =45^\circ$．
故 $\angle C=45^\circ,\angle B=75^\circ$．
故 $\angle ANK=\dfrac{1}{2}\angle KPA=30^\circ$．设 $\angle ACB=\angle NMC=\alpha$．则 $\angle ABC=\angle KMB=120^\circ-\alpha$．
所以，$\angle KMN=60^\circ$，即 $\triangle KMN$ 为等边三角形．
于是，$\angle ANM=90^\circ,\alpha =45^\circ$．
故 $\angle C=45^\circ,\angle B=75^\circ$．
答案
解析
备注
