求证：从椭圆焦点出发的光线经光滑的椭圆壁反射后必经过另一个焦点．你还知道其他圆锥曲线的光学性质吗？请叙述但不必证明．
【难度】
【出处】
2000年复旦大学保送生招生测试
【标注】
【答案】
证明略；其他圆锥曲线的光学性质：
双曲线：从焦点发射的光线，其反射光线的反向延长线经过另一焦点．
抛物线：从焦点发射的光线，其反射光线与轴平行
双曲线：从焦点发射的光线，其反射光线的反向延长线经过另一焦点．
抛物线：从焦点发射的光线，其反射光线与轴平行
【解析】
设椭圆方程为 $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$，如图．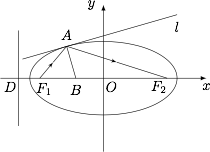
设光线经过 $A$ 点，$l$ 是过 $A$ 点的椭圆的切线，连接 $A{F_2}$，作 $\angle {F_1}A{F_2}$ 的角平分线交 $x$ 轴于 $B$，只需证明 $AB \perp l$．
不妨设 $A(p,q)$ 在椭圆的上半部分，切线的斜率为 ${k_l} =- \dfrac{{p{b^2}}}{{q{a^2}}}$．
设 $A$ 到椭圆的左、右准线的距离分别为 ${h_1},{h_2}$，则$$\dfrac{{|B{F_1}|}}{{|B{F_2}|}} = \dfrac{{|A{F_1}|}}{{|A{F_2}|}} = \dfrac{{{h_1}}}{{{h_2}}} = \dfrac{{p + \dfrac{{{a^2}}}{c}}}{{\dfrac{{{a^2}}}{c} - p}} = \dfrac{{{a^2} + cp}}{{{a^2} - cp}}.$$于是可得 $B\left( {\dfrac{{{c^2}p}}{{{a^2}}},0} \right)$，$AB$ 的斜率为 ${k_{AB}} = \dfrac{{{a^2}q}}{{{b^2}p}}$．因为$${k_{AB}} \cdot {k_l} =- 1,$$所以 $AB$ 与 $l$ 垂直．
其他圆锥曲线的光学性质：
双曲线：从焦点发射的光线，其反射光线的反向延长线经过另一焦点．
抛物线：从焦点发射的光线，其反射光线与轴平行．
设光线经过 $A$ 点，$l$ 是过 $A$ 点的椭圆的切线，连接 $A{F_2}$，作 $\angle {F_1}A{F_2}$ 的角平分线交 $x$ 轴于 $B$，只需证明 $AB \perp l$．不妨设 $A(p,q)$ 在椭圆的上半部分，切线的斜率为 ${k_l} =- \dfrac{{p{b^2}}}{{q{a^2}}}$．
设 $A$ 到椭圆的左、右准线的距离分别为 ${h_1},{h_2}$，则$$\dfrac{{|B{F_1}|}}{{|B{F_2}|}} = \dfrac{{|A{F_1}|}}{{|A{F_2}|}} = \dfrac{{{h_1}}}{{{h_2}}} = \dfrac{{p + \dfrac{{{a^2}}}{c}}}{{\dfrac{{{a^2}}}{c} - p}} = \dfrac{{{a^2} + cp}}{{{a^2} - cp}}.$$于是可得 $B\left( {\dfrac{{{c^2}p}}{{{a^2}}},0} \right)$，$AB$ 的斜率为 ${k_{AB}} = \dfrac{{{a^2}q}}{{{b^2}p}}$．因为$${k_{AB}} \cdot {k_l} =- 1,$$所以 $AB$ 与 $l$ 垂直．
其他圆锥曲线的光学性质：
双曲线：从焦点发射的光线，其反射光线的反向延长线经过另一焦点．
抛物线：从焦点发射的光线，其反射光线与轴平行．
答案
解析
备注
