在四面体 $ABCD$ 中，棱 $AB,CD$ 的中点分别为 $M,N$，求证：任意一个过 $M,N$ 的平面均将四面体 $ABCD$ 分为体积相等的两个部分．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
若过 $M,N$ 的平面过四面体的整条棱，如 $AB$ 或者 $CD$，原命题显然成立，证明如下．不妨设平面过 $AB$，四面体被分为棱锥 $A-BCN$ 和 $A-BND$，这两个三棱锥底面积相等而且同高，体积相等．
若平面不经过整条棱，不妨设其还与棱 $CD$ 和 $AD$ 有公共点．如图，设平面 $MEN$ 是过 $M,N$ 的任一平面，且该平面交 $BC$ 于 $E$，交 $AD$ 于 $F$，
第一种情况，若 $E,F$ 分别为 $BC,AD$ 的中点，此时 $AC$ 和 $BD$ 都与截面平行．结合 $M$ 是 $AB$ 的中点，容易得到棱锥 $A-ENFM$ 与棱锥 $B-MNFM$ 体积相等．只需要证明 $A-ECN$ 与 $F-BND$ 体积相等即可．把两个锥体与锥体 $A-BCD$ 体积进行比对即可得到，他们都是大锥体体积的 $\frac14$．命题得证．
第二种情况，也就是一般情况，不妨 $MF$，$EN$ 交 $BD$ 的延长线于 $G$．如图．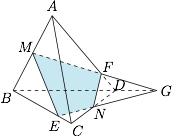
由于 $N$ 是 $CD$ 的中点，所以 $C,D$ 到平面 $MEN$ 的距离相等，从而棱锥 $C-MENF$ 的体积与棱锥 $D-MENF$ 的体积相等．设四面体 $ABCD$ 的体积为 $V$，则\[V_{C-AMF}=\dfrac{AM\cdot AF}{AB\cdot AD}V=\dfrac 12\cdot\dfrac{AF}{AD}V,\]同理，有\[V_{D-BME}=\dfrac 12\cdot \dfrac{BE}{BC}V,\]由梅涅劳斯定理，有\[\dfrac{DG}{GB}\cdot \dfrac{BM}{MA}\cdot \dfrac{AF}{FD}=1,\dfrac{DG}{GB}\cdot \dfrac{BE}{EC}\cdot \dfrac{CN}{ND}=1,\]又\[\dfrac{BM}{MA}=\dfrac{CN}{ND}=1,\]于是\[\dfrac{AF}{FD}=\dfrac{BE}{EC},\]故 $\dfrac{AF}{AD}=\dfrac{BE}{BC}$，这样我们就得到了三棱锥 $C-AMF$ 与三棱锥 $D-BME$ 的体积相等．将体积相等的两组三棱锥对应相加，即得欲证明命题．
若平面不经过整条棱，不妨设其还与棱 $CD$ 和 $AD$ 有公共点．如图，设平面 $MEN$ 是过 $M,N$ 的任一平面，且该平面交 $BC$ 于 $E$，交 $AD$ 于 $F$，
第一种情况，若 $E,F$ 分别为 $BC,AD$ 的中点，此时 $AC$ 和 $BD$ 都与截面平行．结合 $M$ 是 $AB$ 的中点，容易得到棱锥 $A-ENFM$ 与棱锥 $B-MNFM$ 体积相等．只需要证明 $A-ECN$ 与 $F-BND$ 体积相等即可．把两个锥体与锥体 $A-BCD$ 体积进行比对即可得到，他们都是大锥体体积的 $\frac14$．命题得证．
第二种情况，也就是一般情况，不妨 $MF$，$EN$ 交 $BD$ 的延长线于 $G$．如图．
由于 $N$ 是 $CD$ 的中点，所以 $C,D$ 到平面 $MEN$ 的距离相等，从而棱锥 $C-MENF$ 的体积与棱锥 $D-MENF$ 的体积相等．设四面体 $ABCD$ 的体积为 $V$，则\[V_{C-AMF}=\dfrac{AM\cdot AF}{AB\cdot AD}V=\dfrac 12\cdot\dfrac{AF}{AD}V,\]同理，有\[V_{D-BME}=\dfrac 12\cdot \dfrac{BE}{BC}V,\]由梅涅劳斯定理，有\[\dfrac{DG}{GB}\cdot \dfrac{BM}{MA}\cdot \dfrac{AF}{FD}=1,\dfrac{DG}{GB}\cdot \dfrac{BE}{EC}\cdot \dfrac{CN}{ND}=1,\]又\[\dfrac{BM}{MA}=\dfrac{CN}{ND}=1,\]于是\[\dfrac{AF}{FD}=\dfrac{BE}{EC},\]故 $\dfrac{AF}{AD}=\dfrac{BE}{BC}$，这样我们就得到了三棱锥 $C-AMF$ 与三棱锥 $D-BME$ 的体积相等．将体积相等的两组三棱锥对应相加，即得欲证明命题．
答案
解析
备注
