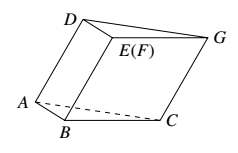
图 $1$ 是由矩形 $ADEB,Rt\triangle ABC$ 和菱形 $BFGC$ 组成的一个平面图形,其中 $AB=1,BE=BF=2,\angle FBC=60^\circ$,将其沿 $AB,BC$ 折起来使得 $BE$ 与 $BF$ 重合,连结 $DG$,如下图.
(1)证明:图 $2$ 中的 $A,C,G,D$ 四点共面,且平面 $ABC\perp$ 平面 $BCGE$;
(2)求图 $2$ 中的四边形 $ACGD$ 的面积.
(1)证明:图 $2$ 中的 $A,C,G,D$ 四点共面,且平面 $ABC\perp$ 平面 $BCGE$;
(2)求图 $2$ 中的四边形 $ACGD$ 的面积.


【难度】
【出处】
2019年高考全国III卷(文)
【标注】
【答案】
略
【解析】
(1)由已知得 $AD\parallel BE,CG\parallel BE$,所以 $AD\parallel CG$,故 $AD,CG$ 确定一个平面,从而 $A,C,G,D$ 四点共面.
由已知得 $AB\perp BE,AB\perp BC$,故 $AB\perp $ 平面 $BCGE$.
又因为 $AB\subset $ 平面 $ABC$,所以平面 $ABC\perp $ 平面 $BCGE$.
(2)取 $CG$ 的中点 $M$,连结 $EM,DM$.
因为 $AB\parallel DE$,$AB\perp $ 平面 $BCGE$,所以 $DE\perp $ 平面 $BCGE$,故 $DE\perp CG$.
由已知,四边形 $BCGE$ 的菱形,且 $\angle EBC=60^\circ$ 得 $EM\perp CG$,故 $CG\perp$ 平面 $DEM$.
因此 $DM\perp CG$.
在 $Rt\triangle DEM$ 中,$DE=1,EM=\sqrt{3}$,故 $DM=2$.
所以四边形 $ACGD$ 的面积为 $4$.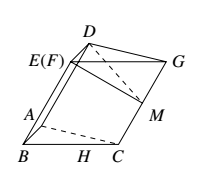
由已知得 $AB\perp BE,AB\perp BC$,故 $AB\perp $ 平面 $BCGE$.
又因为 $AB\subset $ 平面 $ABC$,所以平面 $ABC\perp $ 平面 $BCGE$.
(2)取 $CG$ 的中点 $M$,连结 $EM,DM$.
因为 $AB\parallel DE$,$AB\perp $ 平面 $BCGE$,所以 $DE\perp $ 平面 $BCGE$,故 $DE\perp CG$.
由已知,四边形 $BCGE$ 的菱形,且 $\angle EBC=60^\circ$ 得 $EM\perp CG$,故 $CG\perp$ 平面 $DEM$.
因此 $DM\perp CG$.
在 $Rt\triangle DEM$ 中,$DE=1,EM=\sqrt{3}$,故 $DM=2$.
所以四边形 $ACGD$ 的面积为 $4$.

答案
解析
备注