如图,长方体 $ABCD–A_1B_1C_1D_1$ 的底面 $ABCD$ 是正方形,点 $E$ 在棱 $AA_1$ 上,$BE\perp EC_1$.
(1)证明:$BE\perp $ 平面 $EB_1C_1$;
(2)若 $AE=A_1E,AB=3$,求四棱锥 $E-BB_1C_1C$ 的体积.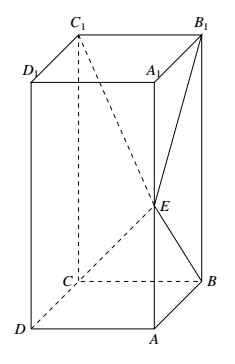
(1)证明:$BE\perp $ 平面 $EB_1C_1$;
(2)若 $AE=A_1E,AB=3$,求四棱锥 $E-BB_1C_1C$ 的体积.

【难度】
【出处】
2019年高考全国II卷(文)
【标注】
【答案】
略
【解析】
(1)由已知得,$B_1C_1\perp$ 平面 $ABB_1A_1$,$BE\subset$ 平面 $ABB_1A_1$,故 $B_1C_1\perp BE$.
又 $BE\perp EC_1$,所以 $BE\perp $ 平面 $EB_1C_1$.
(2)由(1)知 $\angle BEB_1=90^\circ$.由题设知 $Rt\triangle ABE\cong Rt\triangle A_1B_1E$,所以 $\angle AEB=45^\circ$,
故 $AE=AB=3,AA_1=2AE=6$.
所以,四棱锥 $E-BB_1C_1C$ 的体积 $V=\dfrac{1}{3}\times 3\times 6\times 3=18$.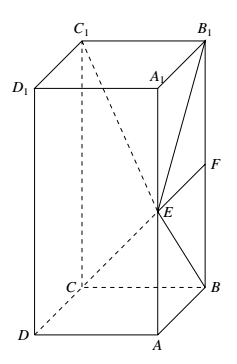
又 $BE\perp EC_1$,所以 $BE\perp $ 平面 $EB_1C_1$.
(2)由(1)知 $\angle BEB_1=90^\circ$.由题设知 $Rt\triangle ABE\cong Rt\triangle A_1B_1E$,所以 $\angle AEB=45^\circ$,
故 $AE=AB=3,AA_1=2AE=6$.
所以,四棱锥 $E-BB_1C_1C$ 的体积 $V=\dfrac{1}{3}\times 3\times 6\times 3=18$.

答案
解析
备注