如图，直四棱柱 $ABCD–A_1B_1C_1D_1$ 的底面是菱形，$AA_1=4,AB=2,\angle BAD=60^\circ$，$E,M,N$ 分别是 $BC,BB_1,A_1D$ 的中点．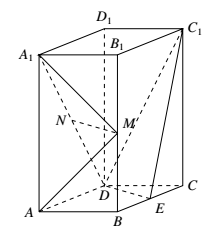
（1）证明：$MN\parallel $ 平面 $C_1DE$；
（2）求点 $C$ 到平面 $C_1DE$ 的距离．
（1）证明：$MN\parallel $ 平面 $C_1DE$；（2）求点 $C$ 到平面 $C_1DE$ 的距离．
【难度】
【出处】
2019年高考全国I卷（文）
【标注】
【答案】
略
【解析】
（1）连结 $B_1C,ME$．
因为 $M,E$ 分别为 $BB_1,BC$ 的中点，
所以 $M\parallel B_1C$，且 $ME=\dfrac{1}{2}B_1C$．
又因为 $N$ 为 $A_1D$ 的中点，所以 $ND=\dfrac{1}{2}A_1D$．
由题设知 $A_1B_1$ 平行且等于 $DC$，可得 $B_1C$ 平行且等于 $A_1D$，故 $ME$ 平行且等于 $ND$，
因此四边形 $MNDE$ 为平行四边形，$MN\parallel ED$．
又 $MN\not\subset$ 平面 $EDC_1$，所以 $MN\parallel$ 平面 $C_1DE$．
（2）过 $C$ 作 $C_1E$ 的垂线，垂足为 $H$．
由已知可得 $DE\perp BC,DE\perp CC_1$，所以 $DE\perp $ 平面 $C_1CE$，故 $DE\perp CH$．
从而 $CH\perp $ 平面 $C_1DE$，故 $CH$ 的长即为 $C$ 到平面 $C_1DE$ 的距离．
由已知可得 $CE=1,CC_1=4$，所以 $C_1E=\sqrt{17}$，故 $CH=\dfrac{4\sqrt{17}}{17}$．
从而点 $C$ 到平面 $C_1DE$ 的距离为 $\dfrac{4\sqrt{17}}{17}$．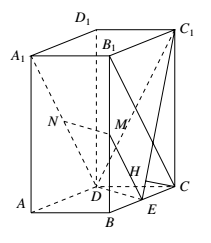
因为 $M,E$ 分别为 $BB_1,BC$ 的中点，
所以 $M\parallel B_1C$，且 $ME=\dfrac{1}{2}B_1C$．
又因为 $N$ 为 $A_1D$ 的中点，所以 $ND=\dfrac{1}{2}A_1D$．
由题设知 $A_1B_1$ 平行且等于 $DC$，可得 $B_1C$ 平行且等于 $A_1D$，故 $ME$ 平行且等于 $ND$，
因此四边形 $MNDE$ 为平行四边形，$MN\parallel ED$．
又 $MN\not\subset$ 平面 $EDC_1$，所以 $MN\parallel$ 平面 $C_1DE$．
（2）过 $C$ 作 $C_1E$ 的垂线，垂足为 $H$．
由已知可得 $DE\perp BC,DE\perp CC_1$，所以 $DE\perp $ 平面 $C_1CE$，故 $DE\perp CH$．
从而 $CH\perp $ 平面 $C_1DE$，故 $CH$ 的长即为 $C$ 到平面 $C_1DE$ 的距离．
由已知可得 $CE=1,CC_1=4$，所以 $C_1E=\sqrt{17}$，故 $CH=\dfrac{4\sqrt{17}}{17}$．
从而点 $C$ 到平面 $C_1DE$ 的距离为 $\dfrac{4\sqrt{17}}{17}$．
答案
解析
备注
