如图,在四棱锥 $P-ABCD$ 中,底面 $ABCD$ 为平行四边形,$\triangle PCD$ 为等边三角形,平面 $PAC\perp $ 平面 $PCD$,$PA\perp CD,CD=2,AD=3$.图片
(I)设 $G,H$ 分别为 $PB,AC$ 的中点,求证:$GH\parallel $ 平面 $PCD$;
(II)求证:$PA\perp $ 平面 $PCD$;
(III)求直线 $AD$ 与平面 $PAC$ 所成角的正弦值.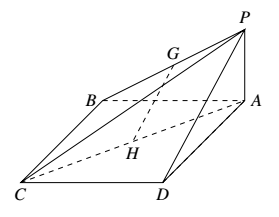
(I)设 $G,H$ 分别为 $PB,AC$ 的中点,求证:$GH\parallel $ 平面 $PCD$;
(II)求证:$PA\perp $ 平面 $PCD$;
(III)求直线 $AD$ 与平面 $PAC$ 所成角的正弦值.

【难度】
【出处】
2019年高考天津卷(文)
【标注】
【答案】
略
【解析】
(I)连接 $BD$,易知 $AC\bigcap BD=H,BH=DH$.又由 $BG=PG$,故 $GH\parallel PD$.又因为 $GH\not\subset $ 平面 $PAD$,$PD\subset$ 平面 $PAD$,所以 $GH\parallel $ 平面 $PAD$.
(II)证明:取棱 $PC$ 的中点 $N$,连接 $DN$,依题意,得 $DN\perp PC$,又因为平面 $PAC\perp $ 平面 $PCD$,平面 $PAC\bigcap $ 平面 $PCD=PC$,所以 $DN\perp $ 平面 $PAC$,又 $PA\subset$ 平面 $PAC$,故 $DN\perp PA$.又已知 $PA\perp CD,CD\bigcap DN=D$,所以 $PA\perp $ 平面 $PCD$.
(III)连接 $AN$,由(II)中 $DN\perp $ 平面 $PAC$,可知 $\angle DAN$ 为直线 $AD$ 与平面 $PAC$ 所成的角.
因为 $\triangle PCD$ 为等边三角形,$CD=2$ 且 $N$ 为 $PC$ 的中点,所以 $DN=\sqrt{3}$,又 $DN\perp AN$,在 $Rt\triangle AND$ 中,$\sin \angle DAN=\dfrac{DN}{AD}=\dfrac{\sqrt{3}}{3}$.
所以,直线 $AD$ 与平面 $PAC$ 所成角的正弦值为 $\dfrac{\sqrt{3}}{3}$.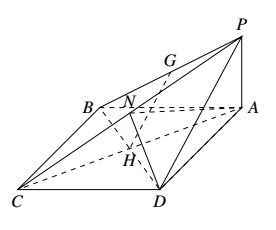
(II)证明:取棱 $PC$ 的中点 $N$,连接 $DN$,依题意,得 $DN\perp PC$,又因为平面 $PAC\perp $ 平面 $PCD$,平面 $PAC\bigcap $ 平面 $PCD=PC$,所以 $DN\perp $ 平面 $PAC$,又 $PA\subset$ 平面 $PAC$,故 $DN\perp PA$.又已知 $PA\perp CD,CD\bigcap DN=D$,所以 $PA\perp $ 平面 $PCD$.
(III)连接 $AN$,由(II)中 $DN\perp $ 平面 $PAC$,可知 $\angle DAN$ 为直线 $AD$ 与平面 $PAC$ 所成的角.
因为 $\triangle PCD$ 为等边三角形,$CD=2$ 且 $N$ 为 $PC$ 的中点,所以 $DN=\sqrt{3}$,又 $DN\perp AN$,在 $Rt\triangle AND$ 中,$\sin \angle DAN=\dfrac{DN}{AD}=\dfrac{\sqrt{3}}{3}$.
所以,直线 $AD$ 与平面 $PAC$ 所成角的正弦值为 $\dfrac{\sqrt{3}}{3}$.

答案
解析
备注