如图,在四棱锥 $P-ABCD$ 中,$PA\perp $ 平面 $ABCD$,底面 $ABCD$ 为菱形,$E$ 为 $CD$ 的中点.
(I)求证:$BD\perp $ 平面 $PAC$;
(II)若 $\angle ABC=60^\circ$,求证:平面 $PAB\perp $ 平面 $PAE$;
(III)棱 $PB$ 上是否存在 $F$,使得 $CF\parallel$ 平面 $PAE$?说明理由.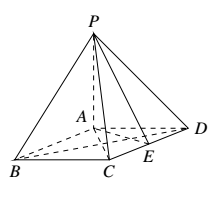
(I)求证:$BD\perp $ 平面 $PAC$;
(II)若 $\angle ABC=60^\circ$,求证:平面 $PAB\perp $ 平面 $PAE$;
(III)棱 $PB$ 上是否存在 $F$,使得 $CF\parallel$ 平面 $PAE$?说明理由.

【难度】
【出处】
2019年高考北京卷(文)
【标注】
【答案】
略
【解析】
(I)因为 $PA\perp $ 平面 $ABCD$,所以 $PA\perp BD$.
又因为底面 $ABCD$ 为菱形,所以 $BD\perp AC$.
所以 $BD\perp $ 平面 $PAC$.
(II)因为 $PA\perp $ 平面 $ABCD$,$AE\subset $ 平面 $ABCD$,所以 $PA\perp AE$.
因为底面 $ABCD$ 为菱形,$\angle ABC=60^\circ$,且 $E$ 为 $CD$ 的中点.
所以 $AE\perp CD$.
所以 $AB\perp AE$.
所以 $AE\perp$ 平面 $PAB$.
所以平面 $PAB\perp $ 平面 $PAE$.
(III)棱 $PB$ 上存在点 $F$,使得 $CF\parallel $ 平面 $PAE$.
取 $F$ 为 $PB$ 的中点,取 $G$ 为 $PA$ 的中点,连结 $CF,FG,EG$.
则 $FG\parallel AB$,且 $FG=\dfrac{1}{2}AB$.
因为底面 $ABCD$ 为菱形,且 $E$ 为 $CD$ 的中点.
所以 $CE\parallel AB$,且 $CE=\dfrac{1}{2}AB$.
所以 $FG\parallel CE$,且 $FG=CE$.
所以四边形 $CEGF$ 为平行四边形.
所以 $CF\parallel EG$.
因为 $CF\not \subset $ 平面 $PAE$,$EG\subset$ 平面 $PAE$.
所以 $CF\parallel $ 平面 $PAE$.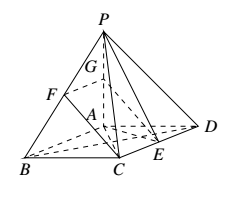
又因为底面 $ABCD$ 为菱形,所以 $BD\perp AC$.
所以 $BD\perp $ 平面 $PAC$.
(II)因为 $PA\perp $ 平面 $ABCD$,$AE\subset $ 平面 $ABCD$,所以 $PA\perp AE$.
因为底面 $ABCD$ 为菱形,$\angle ABC=60^\circ$,且 $E$ 为 $CD$ 的中点.
所以 $AE\perp CD$.
所以 $AB\perp AE$.
所以 $AE\perp$ 平面 $PAB$.
所以平面 $PAB\perp $ 平面 $PAE$.
(III)棱 $PB$ 上存在点 $F$,使得 $CF\parallel $ 平面 $PAE$.
取 $F$ 为 $PB$ 的中点,取 $G$ 为 $PA$ 的中点,连结 $CF,FG,EG$.
则 $FG\parallel AB$,且 $FG=\dfrac{1}{2}AB$.
因为底面 $ABCD$ 为菱形,且 $E$ 为 $CD$ 的中点.
所以 $CE\parallel AB$,且 $CE=\dfrac{1}{2}AB$.
所以 $FG\parallel CE$,且 $FG=CE$.
所以四边形 $CEGF$ 为平行四边形.
所以 $CF\parallel EG$.
因为 $CF\not \subset $ 平面 $PAE$,$EG\subset$ 平面 $PAE$.
所以 $CF\parallel $ 平面 $PAE$.

答案
解析
备注