如图,在平面直角坐标系 $xOy$ 中,椭圆 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$ 的焦点为 $F_1(–1、0),F_2(1,0)$.过 $F_2$ 作 $x$ 轴的垂线 $l$,在 $x$ 轴的上方,$l$ 与圆 $F_2:(x-1)^2+y^2=4a^2$ 交于点 $A$,与椭圆 $C$ 交于点 $D$.连结 $AF_1$ 并延长交圆 $F_2$ 于点 $B$,连结 $BF_2$ 交椭圆 $C$ 于点 $E$,连结 $DF_1$.已知 $DF_1=\dfrac{5}{2}$.
(1)求椭圆 $C$ 的标准方程;
(2)求点 $E$ 的坐标.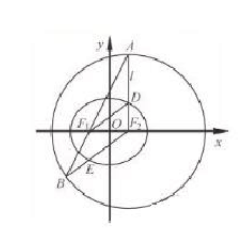
(1)求椭圆 $C$ 的标准方程;
(2)求点 $E$ 的坐标.

【难度】
【出处】
2019年高考江苏卷
【标注】
【答案】
略
【解析】
(1)设椭圆 $C$ 的焦距为 $2c$.
因为 $F_1(-1,0),F_2(1,0)$,所以 $F_1F_2=2,c=1$.
又因为 $DF_1=\dfrac{5}{2}$,$AF_2\perp x$ 轴,所以 $DF_2=\sqrt{DF_1^2-F_1F_2^2}=\sqrt{\left(\dfrac{5}{2}\right)^2-2^2}=\dfrac{3}{2}$,
因此 $2a=DF_1+DF_2=4$,从而 $a=2$.
由 $b^2=a^2-c^2$,得 $b^2=3$.
因此,椭圆 $C$ 的标准方程为 $\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$.
(2)解法一:
由(1)知,椭圆 $C:\dfrac{x^2}{4}+\dfrac{y^2}{3}=1,a=2$,
因为 $AF_2\perp x$ 轴,所以点 $A$ 的横坐标为 $1$.
将 $x=1$ 代入圆 $F_2$ 的方程 $(x-1)^2+y^2=16$,解得 $y=\pm 4$.
因为点 $A$ 在 $x$ 轴上方,所以 $A(1,4)$.
又 $F_1(-1,0)$,所以直线 $AF_1:y=2x+2$.
由 $\begin{cases}y=2x+2\\(x+1)^2+y^2=16\end{cases}$,得 $5x^2+6x-11=0$,
解得 $x=1$ 或 $x=-\dfrac{11}{5}$.
将 $x=-\dfrac{11}{5}$ 代入 $y=2x+2$,得 $y=-\dfrac{12}{5}$,
因此 $B\left(-\dfrac{11}{5},-\dfrac{12}{5}\right)$.又 $F_2(1,0)$,所以直线 $BF_2:y=\dfrac{3}{4}(x-1)$.
由 $\begin{cases}y=\dfrac{3}{4}(x-1)\\\dfrac{x^2}{4}+\dfrac{y^2}{3}=1\end{cases}$,得 $7x^2-6x-13=0$,解得 $x=-1$ 或 $x=\dfrac{13}{7}$.
又因为 $E$ 是线段 $BF_2$ 与椭圆的交点,所以 $x=-1$.
将 $x=-1$ 代入 $y=\dfrac{3}{4}(x-1)$,得 $y=-\dfrac{3}{2}$.因此 $E\left(-1,-\dfrac{3}{2}\right)$.
解法二:
由(1)知,椭圆 $C:\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$.如图,连结 $EF_1$.
因为 $BF_2=2a,EF_1+EF_2=2a$,所以 $EF_1=EB$,从而 $\angle BF_1E=\angle B$.
因为 $F_2A=F_2B$,所以 $\angle A=\angle B$,
所以 $\angle A=\angle BF_1E$,从而 $EF_1\parallel F_2A$.
因为 $AF_2\perp x$ 轴,所以 $EF_1\perp x$ 轴.
因为 $F_1(-1,0)$,由 $\begin{cases}x=-1\\\dfrac{x^2}{4}+\dfrac{y^2}{3}=1\end{cases}$,得 $y=\pm\dfrac{3}{2}$.
又因为 $E$ 是线段 $BF_2$ 与椭圆的交点,所以 $y=-\dfrac{3}{2}$.
因此 $E\left(-1,-\dfrac{3}{2}\right)$.
因为 $F_1(-1,0),F_2(1,0)$,所以 $F_1F_2=2,c=1$.
又因为 $DF_1=\dfrac{5}{2}$,$AF_2\perp x$ 轴,所以 $DF_2=\sqrt{DF_1^2-F_1F_2^2}=\sqrt{\left(\dfrac{5}{2}\right)^2-2^2}=\dfrac{3}{2}$,
因此 $2a=DF_1+DF_2=4$,从而 $a=2$.
由 $b^2=a^2-c^2$,得 $b^2=3$.
因此,椭圆 $C$ 的标准方程为 $\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$.
(2)解法一:
由(1)知,椭圆 $C:\dfrac{x^2}{4}+\dfrac{y^2}{3}=1,a=2$,
因为 $AF_2\perp x$ 轴,所以点 $A$ 的横坐标为 $1$.
将 $x=1$ 代入圆 $F_2$ 的方程 $(x-1)^2+y^2=16$,解得 $y=\pm 4$.
因为点 $A$ 在 $x$ 轴上方,所以 $A(1,4)$.
又 $F_1(-1,0)$,所以直线 $AF_1:y=2x+2$.
由 $\begin{cases}y=2x+2\\(x+1)^2+y^2=16\end{cases}$,得 $5x^2+6x-11=0$,
解得 $x=1$ 或 $x=-\dfrac{11}{5}$.
将 $x=-\dfrac{11}{5}$ 代入 $y=2x+2$,得 $y=-\dfrac{12}{5}$,
因此 $B\left(-\dfrac{11}{5},-\dfrac{12}{5}\right)$.又 $F_2(1,0)$,所以直线 $BF_2:y=\dfrac{3}{4}(x-1)$.
由 $\begin{cases}y=\dfrac{3}{4}(x-1)\\\dfrac{x^2}{4}+\dfrac{y^2}{3}=1\end{cases}$,得 $7x^2-6x-13=0$,解得 $x=-1$ 或 $x=\dfrac{13}{7}$.
又因为 $E$ 是线段 $BF_2$ 与椭圆的交点,所以 $x=-1$.
将 $x=-1$ 代入 $y=\dfrac{3}{4}(x-1)$,得 $y=-\dfrac{3}{2}$.因此 $E\left(-1,-\dfrac{3}{2}\right)$.
解法二:
由(1)知,椭圆 $C:\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$.如图,连结 $EF_1$.
因为 $BF_2=2a,EF_1+EF_2=2a$,所以 $EF_1=EB$,从而 $\angle BF_1E=\angle B$.
因为 $F_2A=F_2B$,所以 $\angle A=\angle B$,
所以 $\angle A=\angle BF_1E$,从而 $EF_1\parallel F_2A$.
因为 $AF_2\perp x$ 轴,所以 $EF_1\perp x$ 轴.
因为 $F_1(-1,0)$,由 $\begin{cases}x=-1\\\dfrac{x^2}{4}+\dfrac{y^2}{3}=1\end{cases}$,得 $y=\pm\dfrac{3}{2}$.
又因为 $E$ 是线段 $BF_2$ 与椭圆的交点,所以 $y=-\dfrac{3}{2}$.
因此 $E\left(-1,-\dfrac{3}{2}\right)$.
答案
解析
备注