如图,一个湖的边界是圆心为 $O$ 的圆,湖的一侧有一条直线型公路 $l$,湖上有桥 $AB$($ AB $ 是圆 $ O $ 的直径).规划在公路 $ l $ 上选两个点 $ P、Q $,并修建两段直线型道路 $ PB、QA $.规划要求:线段 $ PB、QA $ 上的所有点到点 $ O $ 的距离均不小于圆 $ O $ 的半径.已知点 $ A、B $ 到直线 $ l$ 的距离分别为 $AC$ 和 $BD$($C、D$ 为垂足),测得 $AB=10,AC=6,BD=12$(单位:百米).
(1)若道路 $PB$ 与桥 $AB$ 垂直,求道路 $PB$ 的长;
(2)在规划要求下,$P$ 和 $Q$ 中能否有一个点选在 $D$ 处?并说明理由;
(3)在规划要求下,若道路 $PB$ 和 $QA$ 的长度均为 $d$(单位:百米).求当 $d$ 最小时,$P、Q$ 两点间的距离.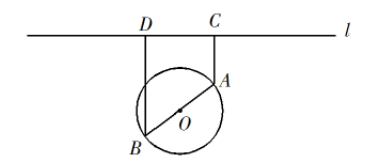
(1)若道路 $PB$ 与桥 $AB$ 垂直,求道路 $PB$ 的长;
(2)在规划要求下,$P$ 和 $Q$ 中能否有一个点选在 $D$ 处?并说明理由;
(3)在规划要求下,若道路 $PB$ 和 $QA$ 的长度均为 $d$(单位:百米).求当 $d$ 最小时,$P、Q$ 两点间的距离.

【难度】
【出处】
2019年高考江苏卷
【标注】
【答案】
略
【解析】
(1)过 $A$ 作 $AE\perp BD$,垂足为 $E$.
由已知条件得,四边形 $ACDE$ 为矩形,$DE=BE=AC=6,AE=CD=8$.
因为 $PB\perp AB$,
所以 $\cos \angle PBD=\sin\angle ABE=\dfrac{8}{10}=\dfrac{4}{5}$.
所以 $PB=\dfrac{BD}{\cos\angle PBD}=\dfrac{12}{\frac{4}{5}}=15$.
因此道路 $PB$ 的长为 $15$(百米).
图1
(2)① 若 $P$ 在 $D$ 处,由(1)可得 $E$ 在圆上,则线段 $BE$ 上的点(除 $B,E$)到点 $O$ 的距离均小于圆 $O$ 的半径,所以 $P$ 选在 $D$ 处不满足规划要求.
② 若 $Q$ 在 $D$ 处,连结 $AD$,由(1)知 $AD=\sqrt{AE^2+ED^2}=10$,
从而 $\cos\angle BAD=\dfrac{AD^2+AB^2-BD^2}{2AD\cdot AB}$,所以 $\angle BAD$ 为锐角.
所以线段 $AD$ 上存在点到点 $O$ 的距离小于圆 $O$ 的半径.
因此,$Q$ 选在 $D$ 处也不满足规划要求.
综上,P和Q均不能选在D处.
(3)先讨论点 $P$ 的位置.
当 $\angle OBP<90^\circ$ 时,线段 $PB$ 上存在点到点 $ O$ 的距离小于圆 $O$ 的半径,点 $P$ 不符合规划要求;
当 $\angle OBP\geqslant 90^\circ$ 时,对线段 $PB$ 上任意一点 $F$,$OF\geqslant OB$,即线段 $PB$ 上所有点到点 $O$ 的距离均不小于圆 $O$ 的半径,点 $P$ 符合规划要求.
设 $P_1$ 为 $l$ 上一点,且 $P_1B\perp AB$,由(1)知,$P_1B=15$,
此时 $P_1D=P_1B\sin\angle P_1BD=P_1B\cos\angle EBA=15\times \dfrac{3}{5}=9$;
当 $\angle OBP>90^\circ$ 时,在 $\triangle PP_1B$ 中,$PB>P_1B=15$.
由上可知,$d\geqslant 15$.
再讨论点 $Q$ 的位置.
由(2)知,要使得 $QA\geqslant 15$,点 $Q$ 只有位于点 $C$ 的右侧,才能符合规划要求.当 $QA=15$ 时,$CQ=\sqrt{QA^2-AC^2}=\sqrt{15^2-6^2}=3\sqrt{21}$.此时,线段 $QA$ 上所有点到点 $O$ 的距离均不小于圆 $O$ 的半径.
综上,当 $PB\perp AB$,点 $Q$ 位于点 $C$ 右侧,且 $CQ=3\sqrt{21}$ 时,$d$ 最小,此时 $P,Q$ 两点间的距离 $PQ=PD+CD+CQ=17+3\sqrt{21}$.
因此,$d$ 最小时,$P,Q$ 两点间的距离为 $17+3\sqrt{21}$(百米).
解法二:
(1)如图,过 $O$ 作 $OH\perp l$,垂足为 $H$.
以 $O$ 为坐标原点,直线 $OH$ 为 $y$ 轴,建立平面直角坐标系.
图2
因为 $BD=12,AC=6$,所以 $OH=9$,直线 $l$ 的方程为 $y=9$,点 $A,B$ 的纵坐标分别为 $3,−3$.
因为 $AB$ 为圆 $O$ 的直径,$AB=10$,所以圆 $O$ 的方程为 $x^2+y^2=25$.
从而 $A(4,3),B(−4,−3)$,直线 $AB$ 的斜率为 $-\dfrac{4}{3}$.
因为 $PB\perp AB$,所以直线 $PB$ 的斜率为 $-\dfrac{4}{3}$,
直线 $PB$ 的方程为 $y=\dfrac{4}{3}x-\dfrac{25}{3}$.
所以 $P(−13,9),PB=\sqrt{(-13+4)^2+(9+3)^2}=15$.
因此道路 $PB$ 的长为 $15$(百米).
(2)① 若 $P$ 在 $D$ 处,取线段 $BD$ 上一点 $E(−4,0)$,则 $EO=4<5$,所以 $P$ 选在 $D$ 处不满足规划要求.
② 若 $Q$ 在 $D$ 处,连结 $AD$,由(1)知 $D(−4,9)$,又 $A(4,3)$,
所以线段 $AD:y=-\dfrac{3}{4}x+6(-4\leqslant x\leqslant x)$.
在线段 $AD$ 上取点 $M\left(3,\dfrac{15}{4}\right)$,因为 $OM=\sqrt{3^2+\left(\dfrac{15}{4}\right)}<\sqrt{3^2+4^2}=5$,
所以线段 $AD$ 上存在点到点 $O$ 的距离小于圆 $O$ 的半径.
因此 $Q$ 选在 $D$ 处也不满足规划要求.
综上,$P$ 和 $Q$ 均不能选在 $D$ 处.
(3)先讨论点 $P$ 的位置.
当 $\angle OBP<90^\circ$ 时,线段 $PB$ 上存在点到点 $O$ 的距离小于圆 $O$ 的半径,点 $P$ 不符合规划要求;
当 $\angle OBP\geqslant 90^\circ$ 时,对线段 $PB$ 上任意一点 $F$,$OF\geqslant OB$,即线段 $PB$ 上所有点到点 $O$ 的距离均不小于圆 $O$ 的半径,点 $P$ 符合规划要求.
设 $P_1$ 为 $l$ 上一点,且 $P_1B\perp AB$,由(1)知,$P_1B=15$,此时 $P_1(−13,9)$;
当 $\angle OBP>90^\circ$ 时,在 $\triangle PP_1B$ 中,$PB>P_1B=15$.
由上可知,$d\geqslant 15$.
再讨论点 $Q$ 的位置.
由(2)知,要使得 $QA\geqslant 15$,点 $Q$ 只有位于点 $C$ 的右侧,才能符合规划要求.当 $QA=15$ 时,设 $Q(a,9)$,由 $AQ=\sqrt{(a-4)^2+(9-3)^2}=15(a>4)$,得 $a=4+3\sqrt{21}$,所以 $Q(4+3\sqrt{21},9)$,此时,线段 $QA$ 上所有点到点 $O$ 的距离均不小于圆 $O$ 的半径.
综上,当 $P(−13,9),Q(4+3\sqrt{21},9)$ 时,$d$ 最小,此时 $P,Q$ 两点间的距离 $PQ=4+3\sqrt{21}-(-13)=17+3\sqrt{21}$.
因此,$d$ 最小时,$P,Q$ 两点间的距离为 $17+3\sqrt{21}$(百米).
由已知条件得,四边形 $ACDE$ 为矩形,$DE=BE=AC=6,AE=CD=8$.
因为 $PB\perp AB$,
所以 $\cos \angle PBD=\sin\angle ABE=\dfrac{8}{10}=\dfrac{4}{5}$.
所以 $PB=\dfrac{BD}{\cos\angle PBD}=\dfrac{12}{\frac{4}{5}}=15$.
因此道路 $PB$ 的长为 $15$(百米).
图1
(2)① 若 $P$ 在 $D$ 处,由(1)可得 $E$ 在圆上,则线段 $BE$ 上的点(除 $B,E$)到点 $O$ 的距离均小于圆 $O$ 的半径,所以 $P$ 选在 $D$ 处不满足规划要求.
② 若 $Q$ 在 $D$ 处,连结 $AD$,由(1)知 $AD=\sqrt{AE^2+ED^2}=10$,
从而 $\cos\angle BAD=\dfrac{AD^2+AB^2-BD^2}{2AD\cdot AB}$,所以 $\angle BAD$ 为锐角.
所以线段 $AD$ 上存在点到点 $O$ 的距离小于圆 $O$ 的半径.
因此,$Q$ 选在 $D$ 处也不满足规划要求.
综上,P和Q均不能选在D处.
(3)先讨论点 $P$ 的位置.
当 $\angle OBP<90^\circ$ 时,线段 $PB$ 上存在点到点 $ O$ 的距离小于圆 $O$ 的半径,点 $P$ 不符合规划要求;
当 $\angle OBP\geqslant 90^\circ$ 时,对线段 $PB$ 上任意一点 $F$,$OF\geqslant OB$,即线段 $PB$ 上所有点到点 $O$ 的距离均不小于圆 $O$ 的半径,点 $P$ 符合规划要求.
设 $P_1$ 为 $l$ 上一点,且 $P_1B\perp AB$,由(1)知,$P_1B=15$,
此时 $P_1D=P_1B\sin\angle P_1BD=P_1B\cos\angle EBA=15\times \dfrac{3}{5}=9$;
当 $\angle OBP>90^\circ$ 时,在 $\triangle PP_1B$ 中,$PB>P_1B=15$.
由上可知,$d\geqslant 15$.
再讨论点 $Q$ 的位置.
由(2)知,要使得 $QA\geqslant 15$,点 $Q$ 只有位于点 $C$ 的右侧,才能符合规划要求.当 $QA=15$ 时,$CQ=\sqrt{QA^2-AC^2}=\sqrt{15^2-6^2}=3\sqrt{21}$.此时,线段 $QA$ 上所有点到点 $O$ 的距离均不小于圆 $O$ 的半径.
综上,当 $PB\perp AB$,点 $Q$ 位于点 $C$ 右侧,且 $CQ=3\sqrt{21}$ 时,$d$ 最小,此时 $P,Q$ 两点间的距离 $PQ=PD+CD+CQ=17+3\sqrt{21}$.
因此,$d$ 最小时,$P,Q$ 两点间的距离为 $17+3\sqrt{21}$(百米).
解法二:
(1)如图,过 $O$ 作 $OH\perp l$,垂足为 $H$.
以 $O$ 为坐标原点,直线 $OH$ 为 $y$ 轴,建立平面直角坐标系.
图2
因为 $BD=12,AC=6$,所以 $OH=9$,直线 $l$ 的方程为 $y=9$,点 $A,B$ 的纵坐标分别为 $3,−3$.
因为 $AB$ 为圆 $O$ 的直径,$AB=10$,所以圆 $O$ 的方程为 $x^2+y^2=25$.
从而 $A(4,3),B(−4,−3)$,直线 $AB$ 的斜率为 $-\dfrac{4}{3}$.
因为 $PB\perp AB$,所以直线 $PB$ 的斜率为 $-\dfrac{4}{3}$,
直线 $PB$ 的方程为 $y=\dfrac{4}{3}x-\dfrac{25}{3}$.
所以 $P(−13,9),PB=\sqrt{(-13+4)^2+(9+3)^2}=15$.
因此道路 $PB$ 的长为 $15$(百米).
(2)① 若 $P$ 在 $D$ 处,取线段 $BD$ 上一点 $E(−4,0)$,则 $EO=4<5$,所以 $P$ 选在 $D$ 处不满足规划要求.
② 若 $Q$ 在 $D$ 处,连结 $AD$,由(1)知 $D(−4,9)$,又 $A(4,3)$,
所以线段 $AD:y=-\dfrac{3}{4}x+6(-4\leqslant x\leqslant x)$.
在线段 $AD$ 上取点 $M\left(3,\dfrac{15}{4}\right)$,因为 $OM=\sqrt{3^2+\left(\dfrac{15}{4}\right)}<\sqrt{3^2+4^2}=5$,
所以线段 $AD$ 上存在点到点 $O$ 的距离小于圆 $O$ 的半径.
因此 $Q$ 选在 $D$ 处也不满足规划要求.
综上,$P$ 和 $Q$ 均不能选在 $D$ 处.
(3)先讨论点 $P$ 的位置.
当 $\angle OBP<90^\circ$ 时,线段 $PB$ 上存在点到点 $O$ 的距离小于圆 $O$ 的半径,点 $P$ 不符合规划要求;
当 $\angle OBP\geqslant 90^\circ$ 时,对线段 $PB$ 上任意一点 $F$,$OF\geqslant OB$,即线段 $PB$ 上所有点到点 $O$ 的距离均不小于圆 $O$ 的半径,点 $P$ 符合规划要求.
设 $P_1$ 为 $l$ 上一点,且 $P_1B\perp AB$,由(1)知,$P_1B=15$,此时 $P_1(−13,9)$;
当 $\angle OBP>90^\circ$ 时,在 $\triangle PP_1B$ 中,$PB>P_1B=15$.
由上可知,$d\geqslant 15$.
再讨论点 $Q$ 的位置.
由(2)知,要使得 $QA\geqslant 15$,点 $Q$ 只有位于点 $C$ 的右侧,才能符合规划要求.当 $QA=15$ 时,设 $Q(a,9)$,由 $AQ=\sqrt{(a-4)^2+(9-3)^2}=15(a>4)$,得 $a=4+3\sqrt{21}$,所以 $Q(4+3\sqrt{21},9)$,此时,线段 $QA$ 上所有点到点 $O$ 的距离均不小于圆 $O$ 的半径.
综上,当 $P(−13,9),Q(4+3\sqrt{21},9)$ 时,$d$ 最小,此时 $P,Q$ 两点间的距离 $PQ=4+3\sqrt{21}-(-13)=17+3\sqrt{21}$.
因此,$d$ 最小时,$P,Q$ 两点间的距离为 $17+3\sqrt{21}$(百米).
答案
解析
备注