如图,在极坐标系中 $Ox$ 中,$A(2,0),B\left(\sqrt{2},\dfrac{\pi}{4}\right),C\left(\sqrt{2},\dfrac{3\pi}{4}\right),D(2,\pi)$,弧 $\overparen{AB},\overparen{BC},\overparen{CD}$ 所在圆的圆心分别是 $(1,0),\left(1,\dfrac{\pi}{2}\right),(1,\pi)$,曲线 $M_1$ 是弧 $\overparen{AB}$,曲线 $M_2$ 是弧 $\overparen{BC}$,曲线 $M_3$ 是弧 $\overparen{CD}$.
(1)分别写出 $M_1,M_2,M_3$ 的极坐标方程;
(2)曲线 $M$ 由 $M_1,M_2,M_3$ 构成,若点 $P$ 在 $M$ 上,且 $|OP|=\sqrt{3}$,求 $P$ 的极坐标.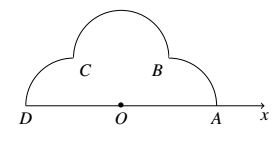
(1)分别写出 $M_1,M_2,M_3$ 的极坐标方程;
(2)曲线 $M$ 由 $M_1,M_2,M_3$ 构成,若点 $P$ 在 $M$ 上,且 $|OP|=\sqrt{3}$,求 $P$ 的极坐标.

【难度】
【出处】
2019年高考全国III卷(理)
【标注】
【答案】
略
【解析】
(1)由题设可得,弧 $\overparen{AB},\overparen{BC},\overparen{CD}$ 所在圆的极坐标方程分别为 $\rho=2\cos\theta,\rho=2\sin\theta,\rho=-2\cos\theta$.
所以 $M_1$ 的极坐标方程为 $\rho=2\cos\theta(0\leqslant \theta\leqslant\dfrac{\pi}{4})$,$M_2$ 的极坐标方程为 $\rho=2\sin\theta(\dfrac{\pi}{4}\leqslant \theta\leqslant \dfrac{3\pi}{4})$,$M_3$ 的极坐标方程为 $\rho=-2\cos\theta(\dfrac{3\pi}{4}\leqslant\theta\leqslant\pi)$.
(2)设 $P(\rho,\theta)$,由题设及(1)知
若 $0\leqslant \theta\leqslant\dfrac{\pi}{4}$,则 $2\cos\theta=\sqrt{3}$,解得 $\theta=\dfrac{\pi}{6}$;
若 $\dfrac{\pi}{4}\leqslant \theta\leqslant \dfrac{3\pi}{4}$,则 $2\sin\theta=\sqrt{3}$,解得 $\theta=\dfrac{\pi}{3}$ 或 $\theta=\dfrac{2\pi}{3}$;
若 $\dfrac{3\pi}{4}\leqslant\theta\leqslant\pi$,则 $-2\cos\theta=\sqrt{3}$,解得 $\theta=\dfrac{5\pi}{6}$.
综上,$P$ 的极坐标为 $\left(\sqrt{3},\dfrac{\pi}{6}\right)$ 或 $\left(\sqrt{3},\dfrac{\pi}{3}\right)$ 或 $\left(\sqrt{3},\dfrac{2\pi}{3}\right)$ 或 $\left(\sqrt{3},\dfrac{5\pi}{6}\right)$.
所以 $M_1$ 的极坐标方程为 $\rho=2\cos\theta(0\leqslant \theta\leqslant\dfrac{\pi}{4})$,$M_2$ 的极坐标方程为 $\rho=2\sin\theta(\dfrac{\pi}{4}\leqslant \theta\leqslant \dfrac{3\pi}{4})$,$M_3$ 的极坐标方程为 $\rho=-2\cos\theta(\dfrac{3\pi}{4}\leqslant\theta\leqslant\pi)$.
(2)设 $P(\rho,\theta)$,由题设及(1)知
若 $0\leqslant \theta\leqslant\dfrac{\pi}{4}$,则 $2\cos\theta=\sqrt{3}$,解得 $\theta=\dfrac{\pi}{6}$;
若 $\dfrac{\pi}{4}\leqslant \theta\leqslant \dfrac{3\pi}{4}$,则 $2\sin\theta=\sqrt{3}$,解得 $\theta=\dfrac{\pi}{3}$ 或 $\theta=\dfrac{2\pi}{3}$;
若 $\dfrac{3\pi}{4}\leqslant\theta\leqslant\pi$,则 $-2\cos\theta=\sqrt{3}$,解得 $\theta=\dfrac{5\pi}{6}$.
综上,$P$ 的极坐标为 $\left(\sqrt{3},\dfrac{\pi}{6}\right)$ 或 $\left(\sqrt{3},\dfrac{\pi}{3}\right)$ 或 $\left(\sqrt{3},\dfrac{2\pi}{3}\right)$ 或 $\left(\sqrt{3},\dfrac{5\pi}{6}\right)$.
答案
解析
备注