如图，几何体是圆柱的一部分，它是矩形 $ABCD$（及其内部）以 $AB$ 边所在直线为旋转轴旋转 $120^{\circ}$ 得到的，$G$ 是 $\widehat{DF}$ 的中点．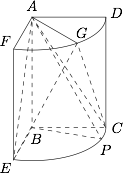
【难度】
【出处】
2017年高考山东卷（理）
【标注】
-
设 $P$ 是 $\widehat {CE}$ 上的一点，且 $AP\perp BE$，求 $\angle CBP$ 的大小；标注答案$30^\circ$解析因为 $AP \perp BE$，$AB\perp BE$，$AB,AP \subset \text{平面}ABP$，$AB\cap AP=A$，所以 $BE \perp \text{平面}ABP$，又 $BP\subset \text{平面}ABP$，所以 $BE \perp BP$，又 $\angle EBC=120^{\circ}$．因此 $\angle CBP=30^{\circ}$．
-
当 $AB=3$，$AD=2$ 时，求二面角 $E-AG-C$ 的大小．标注答案$60^\circ$解析取 $\widehat {BC}$ 的中点 $H$，连接 $EH,GH,CH$．因为 $\angle EBC=120^{\circ}$，所以四边形 $BEHC$ 为菱形，所以$$AE=GE=AC=GC=\sqrt{3^{2}+2^{2}}=\sqrt{13}.$$
取 $AG$ 中点 $M$，连接 $EM,CM,EC$，
则 $EM\perp AG,CM\perp AG$，所以 $\angle EMC$ 为所求二面角的平面角．
又 $AM=1$，所以$$EM=CM=\sqrt{13-1}=2\sqrt 3.$$在 $\triangle BEC$ 中，由于 $\angle EBC=120^{\circ}$，
由余弦定理得\[EC^{2}=2^{2}+2^{2}-2\cdot 2\cdot 2\cdot \cos 120^{\circ}=12,\]所以 $EC=2\sqrt 3$，因此 $\triangle EMC$ 为等边三角形，故所求的角为 $60^{\circ}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
