如图,在三棱锥 $A-BCD$ 中,$AB \perp AD$,$BC\perp BD$,$\mbox {平面}ABD \perp \mbox {平面}BCD$,点 $E$,$F$($E$ 与 $A$,$D$ 不重合)分别在棱 $AD$,$BD$ 上,且 $EF\perp AD$.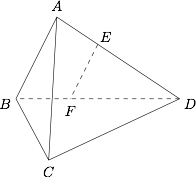

【难度】
【出处】
2017年高考江苏卷
【标注】
-
求证:$EF \parallel \mbox {平面}ABC$;标注答案略解析在平面 $ABD$ 内,因为 $AB\perp AD$,$EF \perp AD$,所以 $EF \parallel AB$.又因为 $EF \not \subset$
平面 $ABC$,$AB \subset$ 平面 $ABC$,所以 $EF\parallel$ 平面 $ABC$. -
求证:$ AD \perp AC $.标注答案略解析因为平面 $ABD \perp$ 平面 $BCD$,平面 $ABD$ 与平面 $BCD$ 的交线为 $BD$,$BC \subset$ 平面 $BCD$,
$BC\perp BD$,所以 $BC \perp$ 平面 $ABD$.因为 $AD \subset$ 平面 $ABD$,所以 $BC\perp AD$.
又 $AB\perp AD$,$BC \cap AB=B$,$AB \subset$ 平面 $ABC$,$BC \subset$ 平面 $ABC$,
所以 $AD \perp$ 平面 $ABC$,又因为 $AC \subset$ 平面 $ABC$,故 $AD \perp AC$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2